Թերմոդինամիկայի մեջ համակարգի սկզբնական վիճակից անցումներն ուսումնասիրելիս կարևոր է իմանալ գործընթացի ջերմային ազդեցությունը: Ջերմային հզորության հայեցակարգը սերտորեն կապված է այս ազդեցության հետ: Այս հոդվածում մենք կքննարկենք այն հարցը, թե ինչ է նշանակում գազի իզոխորիկ ջերմունակություն:
Իդեալական գազ
Իդեալական գազն այն գազն է, որի մասնիկները համարվում են նյութական կետեր, այսինքն՝ չափեր չունեն, բայց զանգված ունեն, և որում ամբողջ ներքին էներգիան բաղկացած է բացառապես մոլեկուլների շարժման կինետիկ էներգիայից։ և ատոմներ։
Իդեալականորեն ցանկացած իրական գազ երբեք չի բավարարի նկարագրված մոդելին, քանի որ դրա մասնիկները դեռևս ունեն որոշ գծային չափեր և փոխազդում են միմյանց հետ՝ օգտագործելով թույլ վան դեր Վալսի կապերը կամ այլ տեսակի քիմիական կապերը: Այնուամենայնիվ, ցածր ճնշման և բարձր ջերմաստիճանի դեպքում մոլեկուլների միջև հեռավորությունները մեծ են, և նրանց կինետիկ էներգիան տասնյակ անգամ գերազանցում է պոտենցիալ էներգիան: Այս ամենը հնարավորություն է տալիս բարձր ճշգրտությամբ կիրառել իրական գազերի իդեալական մոդելը։
Գազի ներքին էներգիա
Ցանկացած համակարգի ներքին էներգիան ֆիզիկական բնութագիր է, որը հավասար է պոտենցիալ և կինետիկ էներգիայի գումարին։ Քանի որ պոտենցիալ էներգիան կարող է անտեսվել իդեալական գազերում, մենք կարող ենք դրանց հավասարությունը գրել՝
U=Ek.
Որտեղ Ek-ը կինետիկ համակարգի էներգիան է: Օգտագործելով մոլեկուլային կինետիկ տեսությունը և կիրառելով Կլապեյրոն-Մենդելեև վիճակի համընդհանուր հավասարումը, դժվար չէ ստանալ U-ի արտահայտությունը: Ստորև գրված է.
U=z/2nRT.
Այստեղ T, R և n-ը համապատասխանաբար բացարձակ ջերմաստիճանն են, գազի հաստատունը և նյութի քանակը: Z-արժեքը ամբողջ թիվ է, որը ցույց է տալիս գազի մոլեկուլի ազատության աստիճանների թիվը:
Իզոբարային և իզոխորային ջերմունակություն
Ֆիզիկայի մեջ ջերմային հզորությունը ջերմության այն քանակությունն է, որը պետք է տրամադրվի ուսումնասիրվող համակարգին՝ այն մեկ կելվինով տաքացնելու համար: Ճիշտ է նաև հակառակ սահմանումը, այսինքն՝ ջերմային հզորությունը ջերմության քանակն է, որն արձակում է համակարգը մեկ կելվինով սառչելիս:
Համակարգի համար ամենահեշտ ձևը իզոխորիկ ջերմային հզորությունը որոշելն է: Այն հասկացվում է որպես ջերմային հզորություն մշտական ծավալով: Քանի որ համակարգը նման պայմաններում աշխատանք չի կատարում, ամբողջ էներգիան ծախսվում է ներքին էներգիայի պաշարների ավելացման վրա։ Իզոխորիկ ջերմունակությունը նշանակենք CV նշանով, այնուհետև կարող ենք գրել.
dU=CVdT.
Այսինքն՝ ներքին էներգիայի փոփոխությունհամակարգը ուղիղ համեմատական է իր ջերմաստիճանի փոփոխությանը: Եթե այս արտահայտությունը համեմատենք նախորդ պարբերությունում գրված հավասարության հետ, ապա կհասնենք CV-ի բանաձևին իդեալական գազի մեջ.
:
СV=z/2nR.
Այս արժեքը գործնականում օգտագործելու համար անհարմար է, քանի որ այն կախված է համակարգում առկա նյութի քանակից: Հետևաբար, ներդրվեց հատուկ իզոխորիկ ջերմային հզորության հայեցակարգը, այսինքն ՝ արժեք, որը հաշվարկվում է կամ 1 մոլ գազի կամ 1 կգ-ի համար: Առաջին արժեքը նշանակենք CV խորհրդանիշով, երկրորդը՝ CV խորհրդանիշով: m. Նրանց համար կարող եք գրել հետևյալ բանաձևերը՝
CV=z/2R;
CVմ=z/2R/M.
Ահա M-ն մոլային զանգվածն է:
Իզոբարը ջերմային հզորությունն է՝ միաժամանակ պահպանելով մշտական ճնշումը համակարգում: Նման գործընթացի օրինակ է գազի ընդլայնումը մխոցի տակ գտնվող բալոնում, երբ այն տաքացվում է: Ի տարբերություն իզոխորիկ պրոցեսի, իզոբար պրոցեսի ժամանակ համակարգին մատակարարվող ջերմությունը ծախսվում է ներքին էներգիան ավելացնելու և մեխանիկական աշխատանք կատարելու համար, այսինքն՝
H=dU + PdV.
Իզոբար պրոցեսի էնթալպիան իզոբարային ջերմային հզորության և համակարգում ջերմաստիճանի փոփոխության արդյունքն է, այսինքն՝
H=CPdT.
Եթե դիտարկենք 1 մոլ գազի մշտական ճնշման ժամանակ ընդլայնումը, ապա թերմոդինամիկայի առաջին օրենքը կգրվի հետևյալ կերպ՝
CPdT=CV dT + RdT.
Վերջին անդամը ստացվում է հավասարումիցԿլապեյրոն-Մենդելեև. Այս հավասարությունից հետևում է իզոբար և իզոխորային ջերմային հզորությունների փոխհարաբերությունները՝
CP=CV + R.
Իդեալական գազի համար մշտական ճնշման դեպքում հատուկ մոլային ջերմային հզորությունը միշտ ավելի մեծ է, քան համապատասխան իզոխորիկ հատկանիշը R=8, 314 Ջ/(մոլԿ):
Մոլեկուլների ազատության և ջերմային հզորության աստիճաններ
Եկեք նորից գրենք հատուկ մոլային իզոխորային ջերմային հզորության բանաձևը՝
CV=z/2R.
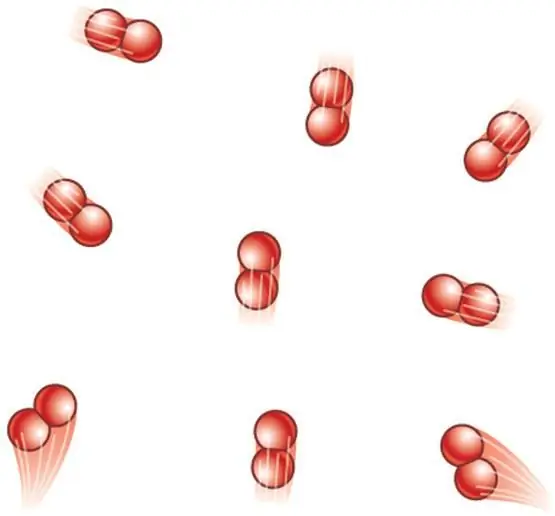
Միատոմ գազի դեպքում z=3 արժեքը, քանի որ տիեզերքում ատոմները կարող են շարժվել միայն երեք անկախ ուղղություններով։
Եթե մենք խոսում ենք երկատոմային մոլեկուլներից բաղկացած գազի մասին, օրինակ՝ թթվածին O2 կամ ջրածին H2, ապա. Բացի թարգմանական շարժումից, այս մոլեկուլները դեռ կարող են պտտվել երկու փոխադարձ ուղղահայաց առանցքների շուրջ, այսինքն՝ z-ը հավասար կլինի 5-ի։
Ավելի բարդ մոլեկուլների համար օգտագործեք z=6:՝ որոշելու համար CV






