Գծային ֆունկցիան մակերևույթի երկայնքով գծված ուղիղ գիծ է: Այն կարելի է բաժանել տարբեր տեսակների և մոդելների։ Ստորև կդիտարկենք դրա ստացման, ինչպես նաև հարթության մեջ դրա կատարելության հասնելու բանաձևերը։ Գծագրերում դուք կարող եք ամբողջությամբ ստուգել դա և հասկանալ, թե ինչպես պետք է այն լինի:
Գծային ֆունկցիա y=kx + b
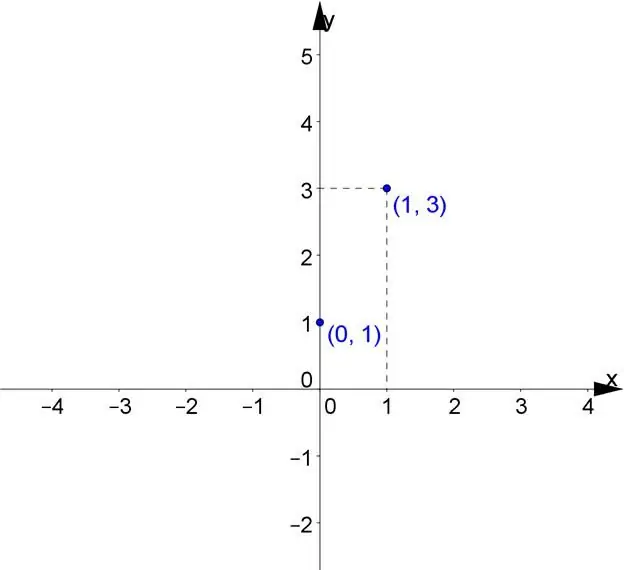
Այս արժեքը փոփոխականի ճշգրիտ չափումն է մեկ տեսքում: Աճը վերաբերում է գծային ֆունկցիայի հիմնական հատկությանը, այն համամասնական է դառնում ավելացող արգումենտին: Այլ կերպ ասած, ֆունկցիան ներկայացնում է ուղիղ համեմատականության ընդհանրացում։ Ուղիղ գիծը գծային ֆունկցիայի գրաֆիկ է: Այստեղից էլ առաջացել է նրա անունը։ Մեկ իրական փոփոխականը շոշափում է մեկ այլ իրական ֆունկցիա:
Հատկություններ
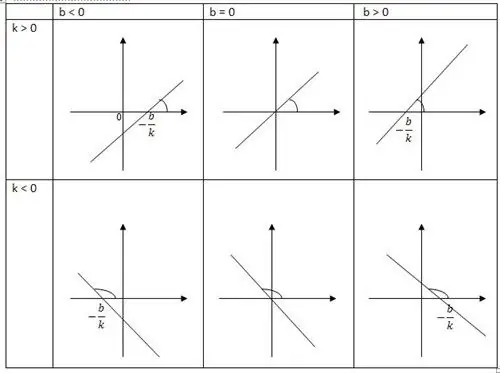
Գծային ֆունկցիան ուղիղ գծի գեներատրից է, որն ունի x առանցքի դրական ուղղությունը: Նրա թեքության որոշիչ գործակիցներից մեկը k-ն է, այն որոշում է a անկյան շոշափողը։ X առանցքի դրական ուղղությամբ ձևավորված ուղիղը k է, մյուս կոորդինատը b ցույց է տալիսկետի կոորդինատները, ինչպես նաև գծի հատումը առանցքի հետ։
Որո՞նք են ոչ գծային ֆունկցիաները:
Ֆունկցիաները, որոնք գծային չեն, կոչվում են ոչ գծային: Սա մաթեմատիկական հարաբերություն է փոփոխականների միջև: Ոչ գծայինները չեն կարող արտահայտվել որպես y=ax + b: Այս տերմինն օգտագործվում է այն պահերին, երբ անհրաժեշտ է ուսումնասիրել ընդհանուր դեպքը։ Այս գործընթացը սկսվում է ցածր աստիճաններից: Այս դեպքում դիտարկվում են քառակուսի ուղղումներ: Նման ֆունկցիան ունի շարունակական կորություն։
Դիտարկվող ոչ գծային հավասարումը կամայական է: Ոչ գծային ֆունկցիայի օրինակ է y=x2: Հաճախ օգտագործվում են «գծային ֆունկցիա» տերմինները՝ ճշգրտումով և «միատարր» բառի ավելացմամբ։ Այն կարող է կիրառվել X-ի ճշգրիտ գծային քարտեզագրման վրա, որը վեկտորային տարածություն է: Գծային ֆունկցիան ամբողջ համակարգն է, ինչպես դա:






