Յուրաքանչյուր մարդ իր կյանքի ընթացքում հանդիպում է մարմինների, որոնք գտնվում են նյութի երեք ընդհանուր վիճակներից մեկում: Ագրեգացման ամենապարզ վիճակն ուսումնասիրելու համար գազն է: Հոդվածում մենք կդիտարկենք իդեալական գազի հայեցակարգը, կտանք համակարգի վիճակի հավասարումը, ինչպես նաև որոշակի ուշադրություն կդարձնենք բացարձակ ջերմաստիճանի նկարագրությանը:
Նյութի գազային վիճակ
Յուրաքանչյուր ուսանող լավ պատկերացնում է, թե նյութի ինչ վիճակի մասին է խոսում, երբ լսում է «գազ» բառը: Այս բառը հասկացվում է որպես մարմին, որն ընդունակ է զբաղեցնել իրեն տրված ցանկացած ծավալ։ Այն ի վիճակի չէ պահպանել իր ձևը, քանի որ չի կարող դիմակայել նույնիսկ ամենաչնչին արտաքին ազդեցությանը։ Նաև գազը չի պահպանում ծավալը, ինչը նրան տարբերում է ոչ միայն պինդ, այլև հեղուկներից։
Ինչպես հեղուկը, գազը հեղուկ նյութ է: Գազերում պինդ մարմինների շարժման գործընթացում վերջիններս խանգարում են այդ շարժմանը։ Ստացված ուժը կոչվում է դիմադրություն: Դրա արժեքը կախված էմարմնի արագությունը գազում։
Գազերի վառ օրինակներն են օդը, բնական գազը, որն օգտագործվում է տների ջեռուցման և ճաշ պատրաստելու համար, իներտ գազերը (Ne, Ar), որոնք օգտագործվում են գովազդային փայլուն խողովակները լցնելու համար կամ օգտագործվում են եռակցման ժամանակ իներտ (ոչ ագրեսիվ, պաշտպանիչ) միջավայր ստեղծելու համար։.
Իդեալական գազ
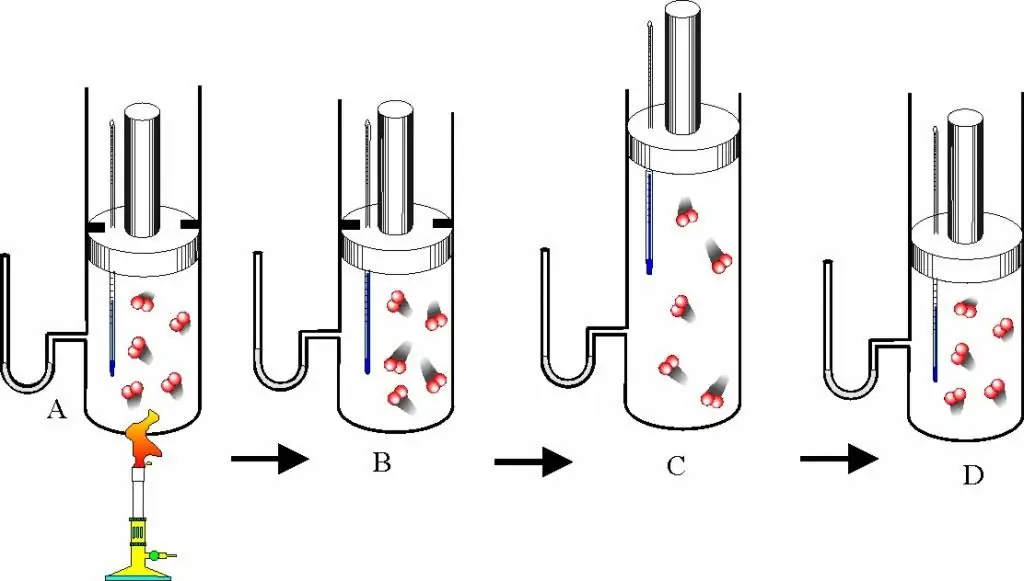
Նախքան գազի օրենքների նկարագրությանը և վիճակի հավասարմանը անցնելը, դուք պետք է լավ հասկանաք այն հարցը, թե ինչ է իդեալական գազը: Այս հայեցակարգը ներդրված է մոլեկուլային կինետիկ տեսության մեջ (MKT): Իդեալական գազ է համարվում ցանկացած գազ, որը բավարարում է հետևյալ բնութագրերը՝
- Այն ձևավորող մասնիկները միմյանց հետ չեն փոխազդում, բացառությամբ ուղղակի մեխանիկական բախումների:
- Անոթի պատերին կամ իրենց միջև մասնիկների բախման արդյունքում պահպանվում են դրանց կինետիկ էներգիան և իմպուլսը, այսինքն՝ բախումը համարվում է բացարձակ առաձգական։
- Մասնիկները չափեր չունեն, բայց ունեն վերջավոր զանգված, այսինքն՝ նման են նյութական կետերին։
Բնական է, որ ցանկացած գազ իդեալական չէ, այլ իրական։ Այնուամենայնիվ, շատ գործնական խնդիրներ լուծելու համար այս մոտարկումները բավականին հիմնավոր են և կարող են օգտագործվել: Կա ընդհանուր էմպիրիկ կանոն, որն ասում է. անկախ քիմիական բնույթից, եթե գազն ունի սենյակային ջերմաստիճանից բարձր ջերմաստիճան և մթնոլորտային կամ ավելի ցածր ճնշում, ապա այն կարելի է իդեալական համարել բարձր ճշգրտությամբ և կարող է օգտագործվել նկարագրելու համար։ այն.վիճակի իդեալական գազի հավասարման բանաձևը.
Կլապեյրոն-Մենդելեևի օրենք
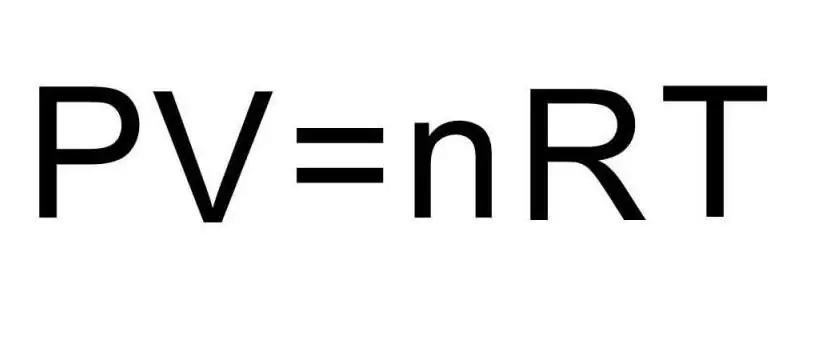
Անցումները նյութի տարբեր ագրեգատային վիճակների և մեկ ագրեգատային վիճակում գտնվող գործընթացների միջև կարգավորվում են թերմոդինամիկայով: Ճնշումը, ջերմաստիճանը և ծավալը երեք մեծություններ են, որոնք եզակիորեն սահմանում են թերմոդինամիկական համակարգի ցանկացած վիճակ: Իդեալական գազի վիճակի հավասարման բանաձևը միավորում է այս երեք մեծությունները մեկ հավասարության մեջ: Եկեք գրենք այս բանաձևը՝
PV=nRT
Այստեղ P, V, T - համապատասխանաբար ճնշում, ծավալ, ջերմաստիճան: n-ի արժեքը նյութի քանակն է մոլերում, իսկ R նշանը նշանակում է գազերի համընդհանուր հաստատունը։ Այս հավասարությունը ցույց է տալիս, որ որքան մեծ է ճնշման և ծավալի արտադրյալը, այնքան մեծ պետք է լինի նյութի քանակի և ջերմաստիճանի արտադրյալը։

Գազի վիճակի հավասարման բանաձևը կոչվում է Կլապեյրոն-Մենդելեև օրենք։ 1834 թվականին ֆրանսիացի գիտնական Էմիլ Կլապեյրոնը, ամփոփելով իր նախորդների փորձարարական արդյունքները, եկավ այս հավասարմանը։ Այնուամենայնիվ, Կլապեյրոնը օգտագործեց մի շարք հաստատուններ, որոնք հետագայում Մենդելեևը փոխարինեց մեկով ՝ ունիվերսալ գազի հաստատուն R (8, 314 J / (մոլԿ)): Ուստի ժամանակակից ֆիզիկայում այս հավասարումն անվանվել է ֆրանսիացի և ռուս գիտնականների անուններով։

Այլ հավասարումների ձևեր
Վերևում մենք գրել ենք Մենդելեև-Կլապեյրոնի վիճակի հավասարումը իդեալական գազի համար ընդհանուր ընդունված ևհարմար ձև: Այնուամենայնիվ, թերմոդինամիկայի խնդիրների դեպքում հաճախ կարող է պահանջվել մի փոքր այլ ձև: Ստորև գրված են ևս երեք բանաձևեր, որոնք ուղղակիորեն բխում են գրավոր հավասարումից՝
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Այս երեք հավասարումները համընդհանուր են նաև իդեալական գազի համար, միայն դրանցում հայտնվում են այնպիսի մեծություններ, ինչպիսիք են m զանգվածը, մոլային զանգվածը M, խտությունը ρ և N մասնիկների թիվը, որոնք կազմում են համակարգը: Այստեղ kB նշանը նշանակում է Բոլցմանի հաստատունը (1, 3810-23J/K):
Բոյլ-Մարիոտի օրենքը
Երբ Կլապեյրոնը կազմեց իր հավասարումը, նա հիմնված էր գազի օրենքների վրա, որոնք փորձնականորեն հայտնաբերվել էին մի քանի տասնամյակ առաջ: Դրանցից մեկը Բոյլ-Մարիոտի օրենքն է։ Այն արտացոլում է իզոթերմային գործընթաց փակ համակարգում, որի արդյունքում փոխվում են այնպիսի մակրոսկոպիկ պարամետրեր, ինչպիսիք են ճնշումը և ծավալը։ Եթե իդեալական գազի վիճակի հավասարման մեջ դնենք T և n հաստատուն, ապա գազի օրենքը կստանա հետևյալ ձևը՝
P1V1=P2V 2
Սա Բոյլ-Մարիոտի օրենքն է, որն ասում է, որ ճնշման և ծավալի արտադրյալը պահպանվում է կամայական իզոթերմ գործընթացի ժամանակ։ Այս դեպքում P և V արժեքներն իրենք են փոխվում:
Եթե գծագրեք P(V) կամ V(P), ապա իզոթերմները կլինեն հիպերբոլաներ:
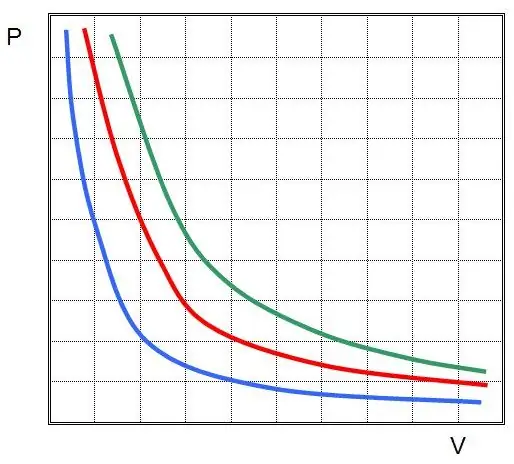
Չարլզի և Գեյ-Լյուսակի օրենքները
Այս օրենքները մաթեմատիկորեն նկարագրում են իզոբարային և իզոխորիկգործընթացներ, այսինքն՝ այնպիսի անցումներ գազային համակարգի վիճակների միջև, որոնցում պահպանվում են համապատասխանաբար ճնշումը և ծավալը։ Չարլզի օրենքը մաթեմատիկորեն կարելի է գրել հետևյալ կերպ՝
V/T=const երբ n, P=const.
Գեյ-Լյուսակի օրենքը գրված է հետևյալ կերպ.
P/T=const երբ n, V=const.
Եթե երկու հավասարություններն էլ ներկայացված են գրաֆիկի տեսքով, ապա մենք կստանանք ուղիղներ, որոնք թեքված են x առանցքի նկատմամբ որոշակի անկյան տակ: Այս տեսակի գծապատկերը ցույց է տալիս ուղիղ համեմատականություն ծավալի և ջերմաստիճանի միջև մշտական ճնշման և ճնշման և ջերմաստիճանի միջև հաստատուն ծավալի դեպքում:
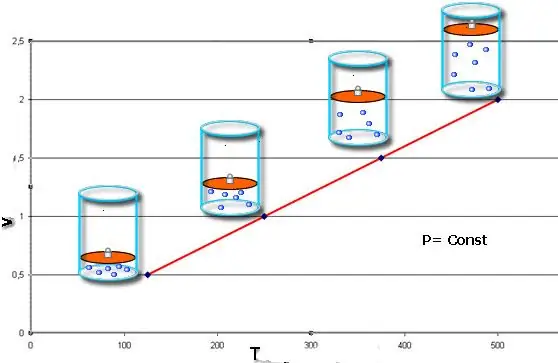
Նշենք, որ գազի բոլոր երեք օրենքները հաշվի չեն առնում գազի քիմիական բաղադրությունը, ինչպես նաև նրա նյութի քանակի փոփոխությունը։
Բացարձակ ջերմաստիճան
Առօրյա կյանքում մենք սովոր ենք օգտագործել Ցելսիուսի ջերմաստիճանի սանդղակը, քանի որ այն հարմար է մեզ շրջապատող գործընթացները նկարագրելու համար։ Այսպիսով, ջուրը եռում է 100 oC և սառչում է 0 oC ջերմաստիճանում: Ֆիզիկայի մեջ այս սանդղակը անհարմար է ստացվում, հետևաբար օգտագործվում է այսպես կոչված բացարձակ ջերմաստիճանի սանդղակը, որը ներմուծել է լորդ Քելվինը 19-րդ դարի կեսերին։ Այս սանդղակի համաձայն՝ ջերմաստիճանը չափվում է Կելվինով (K):
Ենթադրվում է, որ -273, 15 oC ջերմաստիճանի դեպքում ատոմների և մոլեկուլների ջերմային թրթռումներ չկան, նրանց առաջ շարժվելը ամբողջությամբ դադարում է: Այս ջերմաստիճանը Ցելսիուսի աստիճաններով համապատասխանում է բացարձակ զրոյին Կելվինում (0 Կ): Այս սահմանումիցԲացարձակ ջերմաստիճանի ֆիզիկական նշանակությունը հետևյալն է՝ այն նյութը կազմող մասնիկների կինետիկ էներգիայի չափումն է, օրինակ՝ ատոմները կամ մոլեկուլները։
Բացի բացարձակ ջերմաստիճանի վերը նշված ֆիզիկական իմաստից, կան այս մեծությունը հասկանալու այլ մոտեցումներ: Դրանցից մեկը Չարլզի նշված գազային օրենքն է։ Եկեք այն գրենք հետևյալ ձևով՝
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Վերջին հավասարությունն ասում է, որ համակարգում նյութի որոշակի քանակության (օրինակ՝ 1 մոլ) և որոշակի ճնշման (օրինակ՝ 1 Պա) դեպքում գազի ծավալը եզակիորեն որոշում է բացարձակ ջերմաստիճանը։ Այսինքն՝ այս պայմաններում գազի ծավալի ավելացում հնարավոր է միայն ջերմաստիճանի բարձրացման շնորհիվ, իսկ ծավալի նվազումը վկայում է T-ի արժեքի նվազման մասին։
Հիշեցնենք, որ, ի տարբերություն Ցելսիուսի ջերմաստիճանի, բացարձակ ջերմաստիճանը չի կարող բացասական լինել։
Ավոգադրո սկզբունք և գազային խառնուրդներ
Բացի վերը նշված գազային օրենքներից, իդեալական գազի վիճակի հավասարումը հանգեցնում է նաև 19-րդ դարի սկզբին Ամեդեո Ավոգադրոյի հայտնաբերած սկզբունքին, որը կրում է նրա ազգանունը։ Այս սկզբունքը սահմանում է, որ մշտական ճնշման և ջերմաստիճանի դեպքում ցանկացած գազի ծավալը որոշվում է համակարգում առկա նյութի քանակով: Համապատասխան բանաձևն ունի հետևյալ տեսքը՝
n/V=const երբ P, T=const.
Գրավոր արտահայտությունը հանգեցնում է իդեալական գազի ֆիզիկայի մեջ հայտնի Դալթոնի օրենքին գազային խառնուրդների համար: ՍաՕրենքն ասում է, որ գազի մասնակի ճնշումը խառնուրդում եզակիորեն որոշվում է նրա ատոմային մասնաբաժնի միջոցով։
Խնդիրների լուծման օրինակ
Իդեալական գազ պարունակող կոշտ պատերով փակ անոթում տաքացման արդյունքում ճնշումն ավելացել է 3 անգամ։ Անհրաժեշտ է որոշել համակարգի վերջնական ջերմաստիճանը, եթե դրա սկզբնական արժեքը եղել է 25 oC.
Նախ, եկեք ջերմաստիճանը փոխարկենք Ցելսիուսի աստիճանից Քելվինի, մենք ունենք՝
T=25 + 273, 15=298, 15 Կ.
Քանի որ անոթի պատերը կոշտ են, տաքացման գործընթացը կարելի է համարել իզոխորիկ: Այս դեպքում մենք կիրառում ենք Գեյ-Լուսակի օրենքը, ունենք՝
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Այսպիսով, վերջնական ջերմաստիճանը որոշվում է ճնշման հարաբերակցության և սկզբնական ջերմաստիճանի արտադրյալից: Տվյալները փոխարինելով հավասարությամբ՝ ստանում ենք պատասխանը՝ T2=894,45 K: Այս ջերմաստիճանը համապատասխանում է 621,3 oC:






