Մաթեմատիկայում գումարումը (նշվում է մեծ հունական սիգմա նշանով) թվերի գումարելիների բազմություն է։ Որքա՞ն է գումարը: Սա նման գործողության արդյունք է։ Եթե թվերը մեկը մյուսի հետևից գումարվում են ձախից աջ, ապա միջանկյալ արդյունքը մասնակի գումար է։
Որքա՞ն է գումարը։
Ամփոփվող թվերը կարող են լինել ամբողջ, ռացիոնալ, իրական կամ բարդ: Դրանցից բացի կարող են ավելացվել արժեքների այլ տեսակներ՝ վեկտորներ, մատրիցներ, բազմանդամներ և ընդհանրապես ցանկացած հավելումների խմբի (կամ նույնիսկ մոնոիդ) տարրեր։
Եթե տերմինների տարրերի թիվը վերջավոր է, ապա գումարումը միշտ տալիս է լավ սահմանված արժեք: Արժեքների անսահման հաջորդականության գումարումը կոչվում է շարք: Դրա արժեքը հաճախ կարելի է որոշել սահմանի միջոցով (չնայած երբեմն արժեքը կարող է անսահման լինել):
Հաջորդականություններ
[3, 7, 2, 1] թվերի գումարումը կարող է սահմանվել մի արտահայտությամբ, որի արժեքը դրանում ներառված թվանշանների գումարն է, օրինակ՝ 3 + 7 + 2 + 1=13: Քանի որ հավելումԱսոցիատիվորեն, գումարը կախված չէ նրանից, թե ինչպես են տերմինները խմբավորվում, օրինակ՝ (3 + 7) + (2 + 1) և 3 + ((7 + 2) + 1) երկուսն էլ հավասար են ինը, այնպես որ փակագծերը սովորաբար բացակայում են.. Գումարը նույնպես փոխադարձ է, ուստի տերմինների վերադասավորումը չի փոխում գումարի արժեքը: Նկատի ունեցեք, որ այս հատկությունը կարող է չաշխատել անսահման գումարման համար:

Այս կարգի հաջորդականությունների գումարման հատուկ նշում չկա: Կա միայն մի փոքր նրբերանգ, եթե կան երկու տարրից պակաս: Մեկ անդամի հաջորդականության գումարումը գումարած նշան չի պարունակում (այն չի տարբերվում բուն թվի ձևից), և եթե ընդհանրապես տարրեր չկան, ապա այն նույնիսկ չի կարող գրվել (բայց փոխարենը կարելի է նշել. դրա արժեքը «0»): Եթե, այնուամենայնիվ, հաջորդականության պայմանները նշված են որոշակի օրինաչափությամբ, ինչպիսին է ֆունկցիան, ապա գումարման օպերատորը կարող է օգտակար կամ նույնիսկ կարևոր լինել:
Ռեկորդ
Գումարը հասկանալու համար անհրաժեշտ է նաև վերլուծել դրա տեսքը։
1-ից մինչև 100-ը ամբողջ թվերի հաջորդականությունը գումարելու համար հաճախ օգտագործվում է արտահայտություն, որն իր մեջ ներառում է բացակայող անդամները նշելու էլիպսիս՝ 1 + 2 + 3 + 4 + … + 99 + 100: Օրինակը հետևյալն է. բավականին հեշտ է տեսնել այս օրինակում: Այնուամենայնիվ, ավելի բարդ տարբերակների համար անհրաժեշտ է ճշգրիտ նշել այն կանոնը, որն օգտագործվում է տարրերի արժեքը գտնելու համար, որը կարելի է ձեռք բերել «Σ» գումարման օպերատորի միջոցով: Օգտագործելով այս նշանը (սիգմա), կարող եք կիրառել հետևյալ նշումը՝
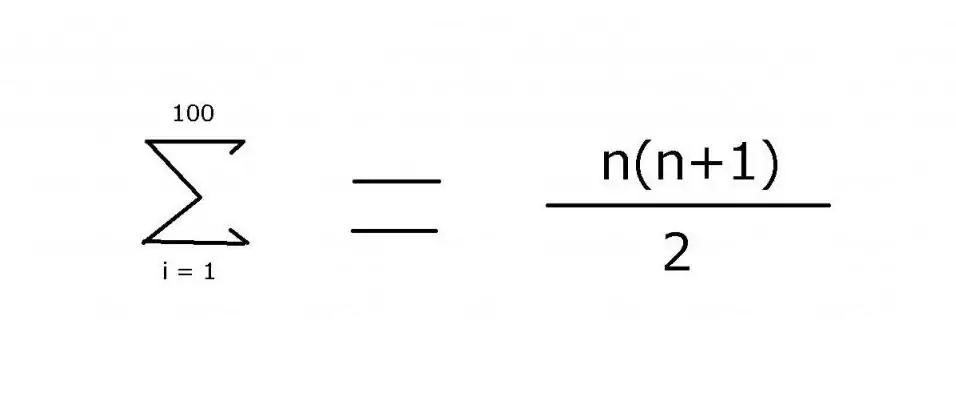
Այս արտահայտության արժեքը 5050 է: Այն կարելի է գտնել մաթեմատիկական ինդուկցիայի միջոցով, որտեղից էլ առաջացել է բանաձևի երկրորդ մասը:
Տարբեր հաջորդականությունների համար բանաձևը կփոխվի: Ձայնագրման գործընթացը կրճատվում է ինչ-որ անսահման հաջորդականության նախնական պատկերի որոնմամբ և այն բանաձևով նկարագրելով: Դա անելուց հետո դժվար չէ հասկանալ, թե կոնկրետ դեպքում որքան է գումարը։
Երբ անհրաժեշտ է պարզաբանել, որ թվերը գումարվում են իրենց նշանների հետ (գումարած կամ մինուս), օգտագործվում է հանրահաշվական գումար տերմինը: Օրինակ, էլեկտրական շղթայի տեսության մեջ Կիրխհոֆի սխեմայի օրենքները հաշվի են առնում հոսանքների հանրահաշվական գումարը հաղորդիչների ցանցում, որոնք հանդիպում են մի կետում, ինչը հակառակ նշաններ է տալիս հանգույցից ներս և դուրս հոսող հոսանքներին:






