Սխալները չափման արդյունքների շեղումներ են մեծության իրական արժեքից: Փաստացի արժեքը կարող է սահմանվել միայն բազմաթիվ չափումներ կատարելով: Գործնականում դա անհնար է իրականացնել։
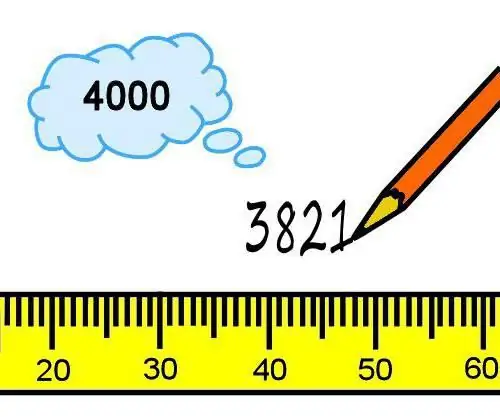
Շեղումների վերլուծության համար իրական արժեքին ամենամոտ արժեքը համարվում է չափված արժեքի իրական արժեք: Այն ստացվում է բարձր ճշգրտության չափման գործիքների և մեթոդների կիրառմամբ։ Չափումների հարմարության, շեղումների վերացման հնարավորությունն ապահովելու համար օգտագործվում են սխալների տարբեր դասակարգումներ։ Դիտարկենք հիմնական խմբերը։
Արտահայտման մեթոդ
Եթե չափիչ գործիքների սխալները դասակարգենք այս հիման վրա, ապա կարող ենք տարբերակել.
- Բացարձակ շեղումներ. Դրանք արտահայտվում են չափվող մեծության միավորներով։
- Հարաբերական շեղում. Այն արտահայտվում է բացարձակ սխալի և չափման արդյունքի հարաբերակցությամբ կամ չափվող մեծության իրական արժեքով։
- Նվազեցված շեղում. Դա արտահայտված հարաբերական սխալն էչափիչ գործիքի բացարձակ շեղման հարաբերակցությունը և որպես հաստատուն ցուցիչ վերցված արժեքը համապատասխան չափման ողջ տիրույթում։ Նրա ընտրությունը հիմնված է ԳՕՍՏ 8.009-84-ի վրա։
Շատ չափիչ գործիքների համար սահմանվել է ճշգրտության դաս: Տրված սխալը ներկայացվում է, քանի որ հարաբերական արժեքը բնութագրում է շեղումը միայն սանդղակի որոշակի կետում և կախված է չափված արժեքի պարամետրից։

Պայմաններ և աղբյուրներ
Սխալների դասակարգման մեջ հիմնական և լրացուցիչ շեղումները առանձնանում են ըստ այս չափանիշների։
Առաջինը չափիչ գործիքների սխալներն են սովորական օգտագործման պայմաններում: Հիմնական շեղումները պայմանավորված են փոխակերպման ֆունկցիայի անկատարությամբ, սարքերի հատկությունների անկատարությամբ։ Դրանք արտացոլում են սովորական պայմաններում սարքի իրական փոխակերպման ֆունկցիայի և անվանականի միջև տարբերությունը (սահմանված է կարգավորող փաստաթղթերում (տեխնիկական պայմաններ, ստանդարտներ և այլն):
Լրացուցիչ սխալներ են առաջանում, երբ արժեքը շեղվում է նորմայից կամ նորմալացված տարածքի սահմաններից դուրս գալու պատճառով:
Նորմալ պայմաններ
Նորմատիվ փաստաթղթերում սահմանված են հետևյալ նորմալ պարամետրերը՝
- Օդի ջերմաստիճան 20±5 deg.
- Հարաբերական խոնավություն 65±15%.
- Ցանցի լարում 220±4, 4 V.
- Հոսանքի հաճախականություն 50±1Հց։
- Ոչ մագնիսական կամ էլեկտրական դաշտեր։
- Սարքի հորիզոնական դիրքը ±2 աստիճան շեղումով։
Ճշգրտության դաս
Շեղումների հանդուրժողականության սահմանները կարող են արտահայտվել հարաբերական, բացարձակ կամ կրճատված սխալներով: Որպեսզի կարողանանք ընտրել ամենահարմար չափիչ գործիքը, համեմատություն է կատարվում ըստ դրանց ընդհանրացված բնութագրի՝ ճշգրտության դասի։ Որպես կանոն, դա թույլատրելի հիմնական և լրացուցիչ շեղումների սահմանն է։

Ճշգրտության դասը թույլ է տալիս հասկանալ նույն տեսակի չափիչ գործիքների սխալների սահմանները: Այնուամենայնիվ, այն չի կարող դիտվել որպես յուրաքանչյուր նման գործիքի կողմից իրականացվող չափումների ճշգրտության ուղղակի ցուցիչ: Փաստն այն է, որ չափման սխալների դասակարգման վրա ազդում են նաև այլ գործոններ (պայմաններ, մեթոդ և այլն): Այս հանգամանքը պետք է հաշվի առնել չափիչ գործիք ընտրելիս՝ կախված փորձի համար սահմանված ճշգրտությունից։
Ճշգրտության դասի արժեքը արտացոլվում է տեխնիկական պայմաններում, ստանդարտներում կամ այլ կարգավորող փաստաթղթերում: Պահանջվող պարամետրը ընտրվում է ստանդարտ տիրույթից: Օրինակ, էլեկտրամեխանիկական սարքերի համար նորմատիվ են համարվում հետևյալ արժեքները՝ 0, 05, 0, 1, 0, 2 և այլն:
Իմանալով չափիչ գործիքի ճշգրտության դասի արժեքը՝ կարող եք գտնել բացարձակ շեղման թույլատրելի արժեքը չափման տիրույթի բոլոր մասերի համար: Ցուցանիշը սովորաբար կիրառվում է անմիջապես սարքի մասշտաբի վրա:
Փոփոխության բնույթը
Այս հատկությունն օգտագործվում է համակարգված սխալների դասակարգման մեջ: Այս շեղումները մնում ենհաստատուն կամ փոփոխվում է որոշակի օրինաչափությունների համաձայն չափումներ կատարելիս: Այս դասակարգման մեջ հատկացրեք սխալների տեսակները, որոնք ունեն համակարգված բնույթ: Դրանք ներառում են՝ գործիքային, սուբյեկտիվ, մեթոդաբանական և այլ շեղումներ։
Եթե համակարգված սխալը մոտենում է զրոյին, ապա այս իրավիճակը կոչվում է կոռեկտություն:
Չափագիտության մեջ չափման սխալների դասակարգման մեջ առանձնանում են նաև պատահական շեղումներ։ Դրանց առաջացումը հնարավոր չէ կանխատեսել։ Պատահական սխալները հաշվետու չեն. դրանք չեն կարող բացառվել չափման գործընթացից: Պատահական սխալները զգալի ազդեցություն ունեն հետազոտության արդյունքների վրա: Շեղումները կարող են կրճատվել կրկնակի չափումների միջոցով՝ արդյունքների հետագա վիճակագրական մշակմամբ: Այլ կերպ ասած, կրկնվող մանիպուլյացիաներից ստացված միջին արժեքը ավելի մոտ կլինի իրական պարամետրին, քան մեկ չափումից ստացվածը: Երբ պատահական շեղումը մոտ է զրոյին, խոսում են չափիչ սարքի ցուցիչների կոնվերգենցիայի մասին։
Դասակարգման սխալների ևս մեկ խումբ՝ բաց թողած: Դրանք, որպես կանոն, կապված են օպերատորի կողմից թույլ տված կամ արտաքին գործոնների ազդեցության համար չհաշվառված սխալների հետ: Սովորաբար բացառվում են չափումների արդյունքները, որոնք հաշվի չեն առնվում ստացված տվյալները մշակելիս:
Կախվածությունը մեծությունից
Շեղումը չի կարող կախված լինել չափված պարամետրից կամ համաչափ լինել դրան: Ըստ այդմ, չափագիտության մեջ սխալների դասակարգման մեջ հավելում ևբազմապատկվող շեղումներ։
Վերջիններս նաև կոչվում են զգայունության սխալներ: Հավելումների շեղումները սովորաբար առաջանում են պիկապների, հենարանների թրթռումների, շփման և աղմուկի պատճառով: Բազմապատկման սխալը կապված է չափիչ գործիքների առանձին մասերի ճշգրտման անկատարության հետ: Դա, իր հերթին, կարող է առաջանալ տարբեր պատճառներով, այդ թվում՝ ֆիզիկական և սարքավորումների հնացած լինելու պատճառով:

Բնութագրերի նորմալացում
Իրականացվում է կախված նրանից, թե որ շեղումն է էական։ Եթե հավելումների սխալը նշանակալի է, սահմանը նորմալացվում է կրճատված շեղման տեսքով, եթե այն բազմապատկվում է, ապա օգտագործվում է փոփոխության հարաբերական մեծության բանաձևը։
Սա նորմալացման մեթոդ է, որի դեպքում երկու ցուցանիշներն էլ համադրելի են, այսինքն՝ թույլատրելի հիմնական տարբերության սահմանն արտահայտվում է երկամյա բանաձևով։ Հետևաբար, ճշտության դասի ցուցիչը նույնպես բաղկացած է 2 թվերից c և d տոկոսներով՝ բաժանված կտրվածքով: Օրինակ՝ 0.2/0.01 Առաջին թիվը արտացոլում է հարաբերական սխալը նորմալ պայմաններում։ Երկրորդ ցուցանիշը բնութագրում է դրա աճը X-ի արժեքի աճով, այսինքն՝ արտացոլում է հավելումների սխալի ազդեցությունը։
Չափված ցուցանիշի փոփոխությունների դինամիկան
Գործնականում օգտագործվում է սխալների դասակարգումը, որն արտացոլում է չափվող քանակի փոփոխությունների բնույթը: Այն ներառում է շեղումների տարանջատում.
- Ստատիկ. Նման սխալներ առաջանում են դանդաղ փոփոխվող կամ չափման ժամանակընդհանրապես չի փոխվում։
- Դինամիկ. Դրանք հայտնվում են ժամանակի ընթացքում արագ փոփոխվող ֆիզիկական մեծություններ չափելիս։
Դինամիկ շեղումը պայմանավորված է սարքի իներցիայով։
Շեղումների գնահատման առանձնահատկությունները
Սխալների վերլուծության և դասակարգման ժամանակակից մոտեցումները հիմնված են սկզբունքների վրա, որոնք ապահովում են համապատասխանությունը չափումների միասնականության պահանջներին:
Գնահատման և հետազոտության նպատակներին հասնելու համար շեղումը նկարագրվում է մոդելի միջոցով (պատահական, գործիքային, մեթոդական և այլն): Այն սահմանում է բնութագրերը, որոնք կարող են օգտագործվել սխալի հատկությունները քանակականացնելու համար: Տեղեկատվության մշակման ընթացքում անհրաժեշտ է գտնել նման բնութագրերի գնահատականներ։

Մոդելն ընտրվում է՝ հաշվի առնելով դրա աղբյուրների տվյալները, այդ թվում՝ փորձի ընթացքում ստացվածները։ Մոդելները բաժանվում են ոչ որոշիչ (պատահական) և դետերմինիստական: Վերջիններս, համապատասխանաբար, հարմար են համակարգված շեղումների համար։
Պատահական սխալի ընդհանուր մոդելն այն արժեքն է, որն իրականացնում է հավանականության բաշխման ֆունկցիան: Շեղման բնութագրերը այս դեպքում բաժանվում են միջակայքի և կետի: Չափման արդյունքների սխալը նկարագրելիս սովորաբար օգտագործվում են ինտերվալային պարամետրեր: Սա նշանակում է, որ սահմանները, որոնց սահմաններում կարող է տեղակայվել շեղումը, սահմանվում են որպես որոշակի հավանականության համապատասխանող: Նման իրավիճակում սահմանները կոչվում են վստահություն, իսկ հավանականությունը՝ համապատասխանաբար վստահություն։
Կետային բնութագրերը օգտագործվում են այն դեպքերում, երբ չկա անհրաժեշտություն կամ հնարավորություն գնահատելու շեղման վստահության սահմանները:
Գնահատման սկզբունքներ
Շեղումների գնահատումներ ընտրելիս օգտագործվում են հետևյալ դրույթները.
- Ընտրված մոդելի անհատական պարամետրերն ու հատկությունները բնութագրվում են: Դա պայմանավորված է նրանով, որ շեղման մոդելներն ունեն բարդ կառուցվածք։ Դրանք նկարագրելու համար օգտագործվում են բազմաթիվ պարամետրեր: Նրանց վճռականությունը հաճախ շատ դժվար է, իսկ որոշ իրավիճակներում նույնիսկ անհնար: Բացի այդ, շատ դեպքերում մոդելի ամբողջական նկարագրությունը պարունակում է ավելորդ տեղեկատվություն, մինչդեռ առանձին բնութագրերի մասին գիտելիքները լիովին բավարար կլինեն առաջադրանքները իրականացնելու և փորձի նպատակներին հասնելու համար:
- Շեղումների գնահատականները որոշվում են մոտավորապես։ Բնութագրերի ճշգրտությունը համապատասխանում է չափումների նպատակին: Դա պայմանավորված է նրանով, որ սխալը բնութագրում է միայն արդյունքի անորոշության գոտին, և դրա վերջնական ճշգրտությունն անհրաժեշտ չէ։
- Շեղումը ավելի լավ է ուռճացնել, քան թերագնահատել: Առաջին դեպքում չափման որակը կնվազի, երկրորդ դեպքում հավանական է ստացված արդյունքների ամբողջական արժեզրկում։

Գնահատեք սխալները չափումից առաջ կամ հետո: Առաջին դեպքում այն կոչվում է a priori, երկրորդում` a posteriori:






