Երբեմն թվում է, թե մեր աշխարհը պարզ է և պարզ: Իրականում սա Տիեզերքի մեծ առեղծվածն է, որը ստեղծել է նման կատարյալ մոլորակ: Կամ գուցե այն ստեղծվել է ինչ-որ մեկի կողմից, ով հավանաբար գիտի, թե ինչ է անում: Մեր ժամանակի մեծագույն ուղեղներն աշխատում են այս հարցի վրա:

Նրանք ամեն անգամ գալիս են այն եզրակացության, որ անհնար է ստեղծել այն ամենը, ինչ մենք ունենք առանց Բարձրագույն մտքի: Ի՜նչ արտասովոր, բարդ և միևնույն ժամանակ պարզ և ուղիղ մեր Երկիր մոլորակը: Մեզ շրջապատող աշխարհը զարմանալի է իր կանոններով, ձևերով, գույներով:
Բնության օրենքներ
Առաջին բանը, որ դուք կարող եք նկատել մեր հսկայական և զարմանալի մոլորակի մասին, առանցքի համաչափությունն է: Այն հանդիպում է շրջապատող աշխարհի բոլոր ձևերում, ինչպես նաև գեղեցկության, իդեալականության և համաչափության հիմնական սկզբունքն է: Սա ոչ այլ ինչ է, քան մաթեմատիկա իր բնույթով:
«Սիմետրիա» հասկացությունը նշանակում է ներդաշնակություն, կոռեկտություն։ Սա շրջապատող իրականության հատկություն է՝ համակարգելով բեկորները և դրանք վերածելով մեկ ամբողջության։ Նույնիսկ Հին Հունաստանում առաջին անգամ սկսեցին նկատել այս օրենքի նշանները։ Օրինակ, Պլատոնը հավատում էր, որ գեղեցկությունը հայտնվում է բացառապեսհամաչափության և համամասնության շնորհիվ։ Իրականում, եթե մենք նայենք առարկաներին, որոնք համաչափ են, ճիշտ և ամբողջական, ապա մեր ներքին վիճակը գեղեցիկ կլինի:
Մաթեմատիկական օրենքները կենդանի և անկենդան բնության մեջ
Եկեք նայենք ցանկացած արարածի, օրինակ՝ ամենակատարյալը՝ տղամարդուն։ Մենք կտեսնենք մարմնի կառուցվածքը, որը երկու կողմից նույն տեսքն ունի։ Կարող եք նաև թվարկել բազմաթիվ նմուշներ, ինչպիսիք են միջատները, կենդանիները, ծովային կենդանիները, թռչունները: Յուրաքանչյուր տեսակ ունի իր գույնը:

Եթե առկա է որևէ նախշ կամ նախշ, ապա հայտնի է, որ դրանք արտացոլված են կենտրոնական գծի շուրջ: Բոլոր օրգանիզմները ստեղծված են տիեզերքի կանոնների շնորհիվ։ Նման մաթեմատիկական օրինաչափությունները կարելի է գտնել անշունչ բնության մեջ:
Եթե ուշադրություն դարձնեք բոլոր երևույթներին, ինչպիսիք են տորնադոն, ծիածանը, բույսերը, ձյան փաթիլները, կարող եք շատ ընդհանրություններ գտնել դրանցում: Ինչ վերաբերում է համաչափության առանցքին, ապա ծառի տերևը կիսով չափ բաժանված է, և յուրաքանչյուր մասը կլինի նախորդի արտացոլումը:

Նաև, եթե որպես օրինակ վերցնենք պտտահողմը, որը բարձրանում է ուղղահայաց և ձագարի տեսք ունի, ապա այն կարելի է նաև պայմանականորեն բաժանել երկու բացարձակապես նույնական կեսերի։ Համաչափության երևույթին կարելի է հանդիպել ցերեկվա և գիշերվա, եղանակների փոփոխության մեջ։ Շրջապատող աշխարհի օրենքները բնության մեջ մաթեմատիկան են, որն ունի իր կատարյալ համակարգը։ Տիեզերքի ստեղծման ողջ հայեցակարգը հիմնված է դրա վրա։
Ծիածան
Մենք հազվադեպ ենք մտածում բնական երևույթների մասին։ Ձյուն եկավ կամ անձրև եկավ, նայեց դուրսարևը կամ ամպրոպը հարվածեց՝ եղանակի փոփոխության սովորական վիճակ: Դիտարկենք մի բազմագույն աղեղ, որը սովորաբար կարելի է գտնել տեղումներից հետո: Երկնքում ծիածանը զարմանալի բնական երևույթ է, որն ուղեկցվում է բոլոր գույների սպեկտրով, որը տեսանելի է միայն մարդու աչքին: Դա տեղի է ունենում արևի ճառագայթների ելքային ամպի միջով անցնելու պատճառով: Անձրևի յուրաքանչյուր կաթիլ ծառայում է որպես պրիզմա, որն օպտիկական հատկություններ ունի: Կարելի է ասել, որ ցանկացած կաթիլ փոքրիկ ծիածան է։

Ջրային պատնեշի միջով անցնելիս ճառագայթները փոխում են իրենց սկզբնական գույնը։ Լույսի յուրաքանչյուր հոսք ունի որոշակի երկարություն և ստվեր: Ուստի մեր աչքն ընկալում է ծիածանը որպես այդպիսի բազմագույն։ Ուշադրություն դարձրեք այն հետաքրքիր փաստին, որ այս երեւույթը կարող է տեսնել միայն մարդը։ Որովհետև դա պարզապես պատրանք է։
Ծիածանների տեսակներ
- Արևից առաջացած ծիածաններն ամենատարածվածն են: Այն ամենապայծառն է բոլոր սորտերից։ Բաղկացած է յոթ հիմնական գույներից՝ կարմիր նարնջագույն, դեղին, կանաչ, կապույտ, ինդիգո, մանուշակագույն: Բայց եթե նայեք մանրամասներին, ապա կան շատ ավելի շատ երանգներ, քան մեր աչքերը կարող են տեսնել:
- Լուսնի կողմից ստեղծված ծիածանը հայտնվում է գիշերը: Ենթադրվում է, որ այն միշտ կարելի է տեսնել: Բայց, ինչպես ցույց է տալիս պրակտիկան, հիմնականում այս երևույթը նկատվում է միայն անձրևոտ տարածքներում կամ մեծ ջրվեժների մոտ: Լուսնի ծիածանի գույները շատ ձանձրալի են: Նրանց վիճակված է դիտարկել միայն հատուկ տեխնիկայի օգնությամբ։ Բայց նույնիսկ դրա հետ մեկտեղ, մեր աչքը կարող է միայն մի սպիտակ շերտ բացահայտել:
- Մառախուղի արդյունքում առաջացած ծիածանը նման է լայն փայլող լուսային կամարի։ Երբեմն այս տեսակը շփոթում են նախորդի հետ: Վերևից գույնը կարող է լինել նարնջագույն, ներքևից կարող է ունենալ մանուշակագույն երանգ։ Արևի ճառագայթները, անցնելով մառախուղի միջով, ձևավորում են գեղեցիկ բնական երևույթ։
- Երկնքում կրակոտ ծիածանը չափազանց հազվադեպ է: Այն իր հորիզոնական տեսքով նման չէ նախորդ տեսակներին։ Դուք կարող եք տեսնել այս երևույթը միայն ցիռուսային ամպերի վերևում: Նրանք սովորաբար տարածվում են 8-10 կիլոմետր բարձրության վրա։ Այն անկյունը, որով ծիածանը կդրսեւորի իրեն իր ողջ փառքով, պետք է լինի ավելի քան 58 աստիճան: Գույները սովորաբար մնում են նույնը, ինչ արևային ծիածանի մեջ։
Ոսկե հարաբերակցություն (1, 618)
Կատարյալ համամասնությունն ամենից հաճախ հանդիպում է կենդանական աշխարհում: Նրանց շնորհվում է այնպիսի համամասնություն, որը հավասար է մեկ PHI-ի համապատասխան թվի արմատին: Այս հարաբերակցությունը մոլորակի բոլոր կենդանիների կապող փաստն է: Հնության մեծ մտքերն այս թիվը անվանեցին աստվածային համամասնություն: Այն կարելի է անվանել նաև ոսկե հարաբերակցություն։
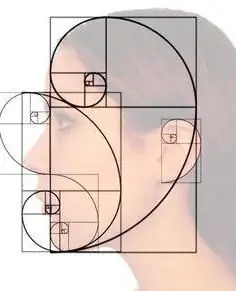
Այս կանոնը լիովին համապատասխանում է մարդու կառուցվածքի ներդաշնակությանը: Օրինակ, եթե որոշեք աչքերի և հոնքերի միջև հեռավորությունը, ապա այն հավասար կլինի աստվածային հաստատունին:
Ոսկե հարաբերակցությունը օրինակ է, թե որքան կարևոր է մաթեմատիկան բնության մեջ, որի օրենքին սկսեցին հետևել դիզայներները, նկարիչները, ճարտարապետները, գեղեցիկ և կատարյալ իրեր ստեղծողները: Նրանք աստվածային հաստատունի օգնությամբ ստեղծում են իրենց ստեղծագործությունները, որոնք հավասարակշռված են, ներդաշնակ և հաճելի դիտելու համար։ Մեր միտքը կարող է հաշվելգեղեցիկ են այն իրերը, առարկաները, երևույթները, որտեղ մասերի անհավասար հարաբերակցություն կա։ Համաչափությունն այն է, ինչ մեր ուղեղն անվանում է ոսկե հարաբերակցություն:
ԴՆԹ պարույր
Ինչպես իրավացիորեն նշել է գերմանացի գիտնական Հյուգո Վեյլը, համաչափության արմատները եկել են մաթեմատիկայի միջոցով: Շատերը նշել են երկրաչափական պատկերների կատարելությունը և ուշադրություն դարձրել դրանց վրա։ Օրինակ, բջիջը ոչ այլ ինչ է, քան վեցանկյուն, որը ստեղծվել է հենց բնության կողմից: Կարելի է ուշադրություն դարձնել նաև եղևնիի կոներին, որոնք ունեն գլանաձև ձև։ Բացի այդ, արտաքին աշխարհում հաճախ հանդիպում է պարույր՝ խոշոր և մանր անասունների եղջյուրներ, խեցեմորթների կեղևներ, ԴՆԹ մոլեկուլներ:

ԴՆԹ պարույրը ստեղծվել է ոսկե հարաբերակցության սկզբունքով։ Այն նյութական մարմնի սխեմայի և նրա իրական պատկերի միջև կապն է: Իսկ եթե հաշվի առնենք ուղեղը, ապա այն ոչ այլ ինչ է, քան հաղորդիչ մարմնի և մտքի միջև։ Ինտելեկտը կապում է կյանքն ու դրա դրսևորման ձևը և թույլ է տալիս ձևի մեջ պարունակվող կյանքը ճանաչել ինքն իրեն։ Դրա օգնությամբ մարդկությունը կարող է հասկանալ շրջապատող մոլորակը, փնտրել դրա մեջ օրինաչափություններ, որոնք այնուհետև կիրառվում են ներաշխարհի ուսումնասիրության համար։
տրոհում բնության մեջ
Բջջային միտոզը բաղկացած է չորս փուլից.
- Պրոֆազ. Այն մեծացնում է միջուկը: Առաջանում են քրոմոսոմներ, որոնք սկսում են ոլորվել պարույրի մեջ և վերածվել իրենց սովորական ձևի։ Բջջային բաժանման համար տեղ է գոյանում։ Ֆազի վերջում միջուկը և դրա թաղանթը լուծվում են, և քրոմոսոմները հոսում են ցիտոպլազմա: Սա բաժանման ամենաերկար փուլն է։
- Մետաֆազ. Այստեղ ավարտվում է քրոմոսոմների պարույրի ոլորումը, նրանք կազմում են մետաֆազային թիթեղ։ Քրոմատիդները շարվում են միմյանց դեմ՝ պատրաստվելով բաժանման։ Նրանց միջև կա անջատման տեղ՝ spindle: Սա ավարտում է երկրորդ փուլը:
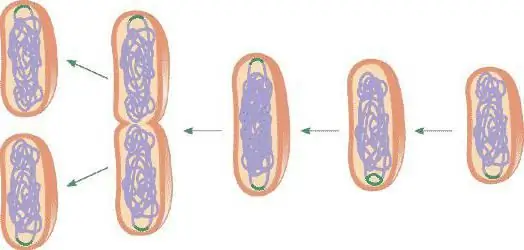
- Անաֆազ. Քրոմատիդները շարժվում են հակառակ ուղղություններով։ Այժմ բջիջն ունի քրոմոսոմների երկու խումբ՝ շնորհիվ դրանց բաժանման։ Այս փուլը շատ կարճ է։
- Telophase. Բջջի յուրաքանչյուր կեսում ձևավորվում է միջուկ, որի ներսում ձևավորվում է միջուկը։ Ցիտոպլազմը ակտիվորեն տարանջատված է: Ափը աստիճանաբար անհետանում է։
Միտոզի նշանակությունը
Բաժանման եզակի մեթոդի շնորհիվ յուրաքանչյուր հաջորդ բջիջ բազմանալուց հետո ունի գեների նույն բաղադրությունը, ինչ իր մայրը: Երկու բջիջների քրոմոսոմների կազմը նույնն է ստանում։ Դա չի կարող անել առանց այնպիսի գիտության, ինչպիսին երկրաչափությունն է: Միտոզի առաջընթացը կարևոր է, քանի որ բոլոր բջիջները վերարտադրվում են այս սկզբունքով:
Որտեղի՞ց են առաջանում մուտացիաները
Այս գործընթացը երաշխավորում է քրոմոսոմների և գենետիկական նյութերի մշտական հավաքածու յուրաքանչյուր բջիջում: Միտոզի պատճառով տեղի է ունենում օրգանիզմի զարգացում, բազմացում, վերածնում։ Որոշ թույների գործողության պատճառով բջիջների բաժանման խախտման դեպքում քրոմոսոմները կարող են չցրվել իրենց կիսով չափ, կամ կարող են զգալ կառուցվածքային խանգարումներ: Սա կլինի սկզբնական մուտացիաների հստակ ցուցիչ:
Ամփոփում
Ի՞նչ ընդհանրություն ունեն մաթեմատիկան և բնությունը: Այս հարցի պատասխանը կգտնեք մեր հոդվածում: Եվ եթե դուք ավելի խորն եք, ապա ձեզ հարկավոր էասել, որ շրջապատող աշխարհն ուսումնասիրելու միջոցով մարդ ճանաչում է իրեն։ Առանց Գերագույն Միտքի, որը ծնեց բոլոր կենդանի էակներին, ոչինչ չէր կարող լինել: Բնությունը բացառապես ներդաշնակ է, իր օրենքների խիստ հաջորդականությամբ։ Այս ամենն առանց պատճառի հնարավո՞ր է։
Եկեք մեջբերենք գիտնական, փիլիսոփա, մաթեմատիկոս և ֆիզիկոս Անրի Պուանկարեի հայտարարությունը, ով, ինչպես ոչ ոք, կկարողանա պատասխանել այն հարցին, թե արդյոք մաթեմատիկան իր բնույթով հիմնարար է։ Որոշ մատերիալիստների նման պատճառաբանությունը կարող է դուր չգալ, բայց դժվար թե նրանք կարողանան հերքել այն։ Պուանկարեն ասում է, որ ներդաշնակությունը, որը մարդկային միտքը ցանկանում է բացահայտել բնության մեջ, չի կարող գոյություն ունենալ դրանից դուրս։ Օբյեկտիվ իրականությունը, որն առկա է առնվազն մի քանի անհատների գիտակցության մեջ, կարող է հասանելի լինել ողջ մարդկությանը: Այն կապը, որը միավորում է մտավոր գործունեությունը, կոչվում է աշխարհի ներդաշնակություն: Վերջին շրջանում նման գործընթացի ճանապարհին ահռելի առաջընթաց է նկատվում, բայց դրանք շատ փոքր են։ Տիեզերքը և անհատը կապող այս կապերը պետք է արժեքավոր լինեն ցանկացած մարդկային մտքի համար, որը զգայուն է այս գործընթացների նկատմամբ:






