Որքան մեծանում են աշակերտները, այնքան ավելի է առաջանում պարզ խնդիրների լուծման արագության կարիքը: Քննություններին շատ ժամանակ չի տրվում պարզ օրինակներ կամ խնդիրներ երկար ժամանակ լուծելու համար։ Ինչպե՞ս արագ և հեշտությամբ գտնել քառակուսու անկյունագիծը: Սա սովորեցնում են ութերորդ դասարանի երեխաներին։ Այս հոդվածը ցույց է տալիս երկու ճանապարհ՝ մեկը ավելի երկար է, մյուսը՝ ավելի արագ։
Ինչպե՞ս հաշվել քառակուսու անկյունագիծը:
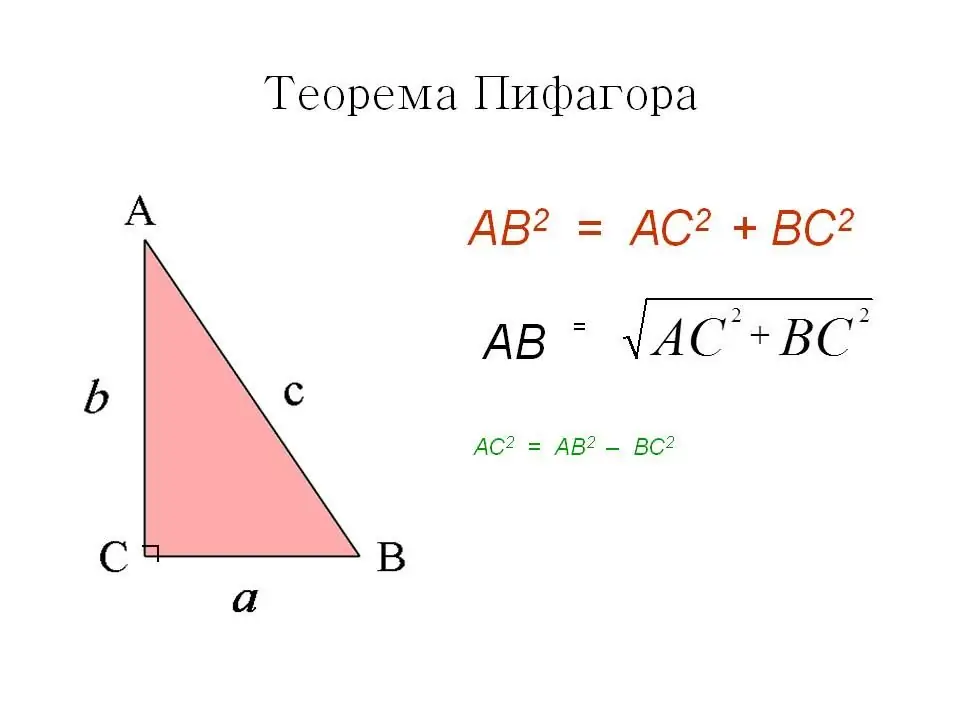
Առաջին ճանապարհը հայտնի և ծանոթ Պյութագորասի թեորեմն է: Քառակուսիում բոլոր անկյունները ուղիղ են, ինչը նշանակում է, որ անկյունագիծը այն բաժանում է երկու հավասար ուղղանկյուն եռանկյունների և ինքնին նրանց հիպոթենուսն է: Պյութագորասի թեորեմի համաձայն՝ հիպոթենուսի քառակուսին հավասար է ոտքերի քառակուսիների գումարին։

Երկրորդ ճանապարհը պարզ բանաձև է, որը հատուկ է քառակուսիներին, և դուք պարզապես պետք է հիշեք այն: Ինչպես գիտեք, քառակուսու բոլոր կողմերը հավասար են, և այդ պատճառով մաթեմատիկոսները հաշվարկել են դրա անկյունագիծը գտնելու հետևյալ բանաձևը. այն հավասար է երկու կողմի և արմատի արտադրյալին։
Իհարկե, ավելի լավ է պարզապես հիշել քառակուսու անկյունագծի երկարության բանաձևը և օգտագործել այն միշտ, քանի որ այն շատ ավելի արագ և հարմար է: Սա հատկապես զգացվում է բառացիորեն խնդիրներ լուծելիս, որտեղ ամբողջ մեծ արմատային արտահայտությունների փոխարեն կարող եք հաղթահարել միայն մեկ ապրանք:
Օրինակ
Վերցրեք, օրինակ, 6-ից 6 քառակուսի, այսինքն՝ վեց սանտիմետր հավասար կողմով:
Առաջին մեթոդի համաձայն՝ անկյունագիծը թող լինի C, իսկ կողմը՝ A։
Այնուհետև մենք ստանում ենք, որ C=√A^2+A^2 կամ C=√2A^2.
Գրենք այն թվային տեսքով՝ С=√36 + 36։ Ստացանք √72, որը 3√8 է կամ 6√2։
Եվ հիմա եկեք գտնենք նույն անկյունագիծը, բայց երկրորդ մեթոդով՝ C=A√2 կամ թվային ձևով՝ 6√2
Այժմ դուք կարող եք տեսնել, թե որքանով է երկրորդ մեթոդն ավելի արագ, հեշտ և ամենակարևորը` ավելի արդյունավետ, հատկապես այսպիսի հեշտ խնդիրների դեպքում, քանի որ քննության ժամանակ յուրաքանչյուր րոպեն թանկ է:
Քառակուսի անկյունագծերի այլ հատկություններ
Բացի այն, թե ինչպես գտնել քառակուսու անկյունագծերը, դուք նաև պետք է իմանաք դրանց հատկությունները: Հիմնականներն են՝
- Անկյունագծերը հավասար են միմյանց, և հատման կետը կիսով չափ բաժանված է:
- Նրանք ուղիղ անկյուններ են կազմում, երբ հատվում են։
- Բաժանիր քառակուսին հավասար եռանկյունների։
Եզրակացություն
Հարց, թե ինչպես կարելի է հաշվել քառակուսու անկյունագծերը, սովորաբար տալիս են այն աշակերտները, ովքեր բաց են թողել այս թեման դպրոցում: Այնուամենայնիվ, բոլորը պետք է իմանան մաթեմատիկայի այսպիսի հիմնարար կանոններ. Ցանկալի է հնարավորինս արագ լուծել, իսկ դա պահանջում է կրճատ բանաձեւերի իմացություն։ Այս ամենը չափազանց պարզ է և հեշտ, բայցմիևնույն ժամանակ դա հիմք է, որն անհրաժեշտ է ապագայում շատ ավելի բարդ խնդիրների լուծման համար։ Եվ այս հիմքի կարևոր մասը քառակուսին է։






