Իզոխորիկ գործընթաց - ինչ է դա:

2024 Հեղինակ: Angel Austin | [email protected]. Վերջին փոփոխված: 2024-01-02 17:49

Գազերը, թերմոդինամիկայի տեսանկյունից, նկարագրվում են մակրոսկոպիկ բնութագրերի մի շարքով, որոնցից հիմնականներն են ջերմաստիճանը, ճնշումը և ծավալը։ Այս պարամետրերից մեկի կայունությունը և մյուս երկուսի փոփոխությունը ցույց են տալիս, որ գազում տեղի է ունենում այս կամ այն իզոպրոցեսը: Այս հոդվածը կնվիրենք այն հարցերի մանրամասն պատասխանին, որ սա իզոխորիկ գործընթաց է, ինչպես է այն տարբերվում գազային համակարգի վիճակներում իզոթերմային և իզոբարային փոփոխություններից:

Իդեալական գազ ֆիզիկայում

Նախքան հարցին պատասխանելը, որ սա իզոխորիկ գործընթաց է, դուք պետք է ավելի լավ ծանոթանաք իդեալական գազի գաղափարին: Ֆիզիկայի մեջ հասկացվում է որպես ցանկացած գազ, որի բաղկացուցիչ մասնիկների միջին կինետիկ էներգիան անհամեմատ գերազանցում է դրանց փոխազդեցության պոտենցիալ էներգիան, և այդ մասնիկների միջև հեռավորությունները մի քանի կարգով ավելի մեծ են, քան դրանց գծային չափերը: Նշված պայմաններում դա հնարավոր է իրականացնելիսհաշվարկներում հաշվի չի առնվում մասնիկների փոխազդեցության էներգիան (այն հավասար է զրոյի), ինչպես նաև կարելի է ենթադրել, որ մասնիկները որոշակի մ զանգված ունեցող նյութական կետեր են։

Իդեալական գազի մեջ տեղի ունեցող միակ գործընթացը մասնիկների բախումն է նյութ պարունակող անոթի պատերին։ Այս բախումները գործնականում դրսևորվում են որպես P գազում որոշակի ճնշման առկայություն.

Որպես կանոն, ցանկացած գազային նյութ, որը բաղկացած է համեմատաբար քիմիապես իներտ մոլեկուլներից և ունի ցածր ճնշում և բարձր ջերմաստիճան, կարող է համարվել իդեալական գազ՝ գործնական հաշվարկների համար բավարար ճշգրտությամբ:

Իդեալական գազը նկարագրող հավասարում

Իհարկե, խոսքը Կլապեյրոն-Մենդելեևի ունիվերսալ օրենքի մասին է, որը պետք է լավ հասկանալ՝ հասկանալու համար, որ սա իզոխորիկ գործընթաց է։ Այսպիսով, վիճակի համընդհանուր հավասարումն ունի հետևյալ ձևը՝

PV=nRT.

Այսինքն՝ P ճնշման և գազի ծավալի արտադրյալը հավասար է T բացարձակ ջերմաստիճանի և նյութի քանակի արտադրյալին մոլներում, որտեղ R-ը համաչափության գործակիցն է։ Հավասարումն ինքնին առաջին անգամ գրվել է Էմիլ Կլապեյրոնի կողմից 1834 թվականին, իսկ 19-րդ դարի 70-ական թվականներին Դ. Մենդելեևը դրանում փոխարինեց R (8,314 J/(molK) մեկ համընդհանուր գազի հաստատունի հաստատուն արժեքների մի շարք։)).

Կլապեյրոն-Մենդելեև հավասարման համաձայն՝ փակ համակարգում գազի մասնիկների թիվը մնում է հաստատուն, հետևաբար կան միայն երեք մակրոսկոպիկ պարամետրեր, որոնք կարող են փոխվել (T, P.և V). Վերջին փաստը ընկած է տարբեր իզոպրեսսների ըմբռնման հիմքում, որոնք կքննարկվեն ստորև:

Ի՞նչ է իզոխորիկ պրոցեսը:

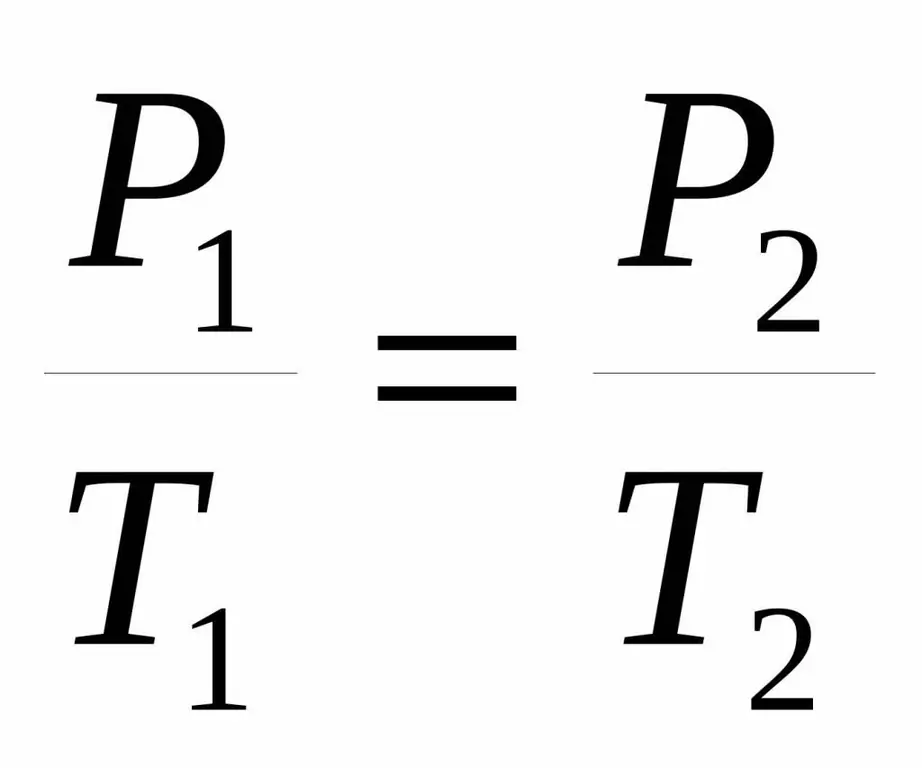
Այս գործընթացը հասկացվում է որպես համակարգի վիճակի բացարձակ ցանկացած փոփոխություն, որում պահպանվում է դրա ծավալը:

Եթե անդրադառնանք վիճակի համընդհանուր հավասարմանը, ապա կարող ենք ասել, որ իզոխորիկ գործընթացում գազում փոխվում է միայն ճնշումը և բացարձակ ջերմաստիճանը: Հստակ հասկանալու համար, թե ինչպես են փոխվում թերմոդինամիկական պարամետրերը, մենք գրում ենք համապատասխան մաթեմատիկական արտահայտությունը՝

P / T=Const.

Երբեմն այս հավասարությունը տրվում է մի փոքր այլ ձևով.

P₁ / T₁=P₂ / T _2.

Երկու հավասարություններն էլ կոչվում են Շառլի օրենք ֆրանսիացի գիտնականի անունով, ով 18-րդ դարի վերջում ստացել է նշված կախվածությունը փորձարարական ճանապարհով:

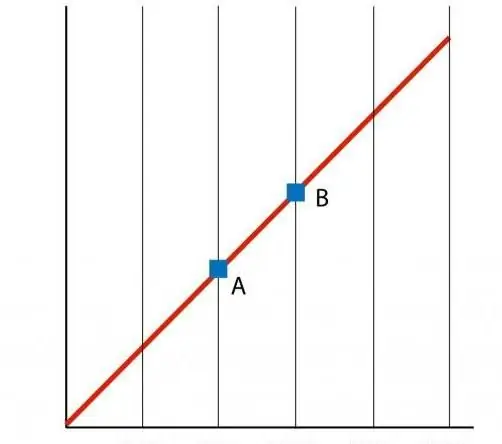
Եթե կառուցենք P(T) ֆունկցիայի գրաֆիկը, ապա կստանանք ուղիղ գծային կախվածություն, որը կոչվում է իզոխոր։ Ցանկացած իզոխոր (n-ի և V-ի բոլոր արժեքների համար) ուղիղ գիծ է:

Գործընթացի էներգետիկ նկարագրություն

Ինչպես նշվեց, իզոխորիկ պրոցեսը համակարգի վիճակի փոփոխությունն է, որը տեղի է ունենում փակ, բայց ոչ մեկուսացված համակարգում: Խոսքը գազի և շրջակա միջավայրի միջև ջերմափոխանակության հնարավորության մասին է։ Ընդհանուր առմամբ, համակարգին Q ջերմության ցանկացած մատակարարում հանգեցնում է երկու արդյունքի՝

• փոխում է ներքին էներգիան U;
• գազաշխատում է A՝ ընդլայնելով կամ կծկվող:

Վերջին եզրակացությունը մաթեմատիկորեն գրված է հետևյալ կերպ.

Q=U + A.

Իդեալական գազի իզոխորիկ գործընթացը, ըստ իր սահմանման, չի ենթադրում գազի կողմից կատարված աշխատանք, քանի որ դրա ծավալը մնում է անփոփոխ: Սա նշանակում է, որ համակարգին մատակարարվող ողջ ջերմությունը գնում է նրա ներքին էներգիան ավելացնելու համար:

Q=U.

Եթե այս արտահայտության մեջ փոխարինենք ներքին էներգիայի հստակ բանաձևը, ապա իզոխորիկ պրոցեսի ջերմությունը կարող է ներկայացվել հետևյալ կերպ՝

Q=z / 2nRT.

Այստեղ z-ն ազատության աստիճանների թիվն է, որը որոշվում է գազը կազմող մոլեկուլների բազմատոմային բնույթով։ Միատոմ գազի համար z=3, երկատոմային գազի համար՝ 5, իսկ եռատոմային և ավելիի համար՝ 6։ Այստեղ ազատության աստիճանների տակ նկատի ունենք փոխադրական և պտտվող աստիճաններ։

Եթե համեմատենք գազի համակարգի ջեռուցման արդյունավետությունը իզոխորիկ և իզոբար գործընթացներում, ապա առաջին դեպքում կստանանք առավելագույն արդյունավետությունը, քանի որ համակարգի վիճակի իզոբար փոփոխության ժամանակ գազը ընդլայնվում է և ջերմության ներդրման մի մասը ծախսվում է աշխատանքի վրա։

Իզոբարային գործընթաց

Վերևում մենք մանրամասն նկարագրեցինք, որ սա իզոխորիկ գործընթաց է: Հիմա մի քանի խոսք ասենք այլ իզոպրոցեսների մասին։ Սկսենք իզոբարից: Անվանման հիման վրա հասկացվում է որպես համակարգի անցում վիճակների միջև մշտական ճնշման տակ։ Այս գործընթացը նկարագրված է Գեյ-Լուսակի օրենքով հետևյալ կերպ՝

V / T=Const.

Ինչպես իզոխորի դեպքում, V(T) իզոբարը նույնպես ուղիղ գիծ է ներկայացնում գրաֆիկի վրա:

ՀանունՑանկացած իզոբար պրոցեսի դեպքում հարմար է հաշվարկել գազի կատարած աշխատանքը, քանի որ այն հավասար է մշտական ճնշման և ծավալի փոփոխության արտադրյալին։

Իզոթերմային գործընթաց

Սա գործընթաց է, որի ժամանակ համակարգի ջերմաստիճանը մնում է հաստատուն: Այն նկարագրված է Բոյլ-Մարիոտի օրենքով իդեալական գազի համար: Հետաքրքիր է նշել, որ սա առաջին փորձարարական հայտնաբերված գազային օրենքն է (17-րդ դարի երկրորդ կես): Դրա մաթեմատիկական նշումն ունի հետևյալ տեսքը՝

PV=Const.

Իզոխորիկ և իզոթերմային գործընթացները տարբերվում են իրենց գրաֆիկական ներկայացմամբ, քանի որ P(V) ֆունկցիան հիպերբոլիկ է, այլ ոչ գծային հարաբերություն:

Խնդիրների լուծման օրինակ

Եկեք համախմբենք հոդվածում ներկայացված տեսական տեղեկատվությունը դրանց կիրառմամբ՝ գործնական խնդիր լուծելու համար։ Հայտնի է, որ մաքուր գազային ազոտը գտնվում էր բալոնում 1 մթնոլորտ ճնշման և 25 °C ջերմաստիճանի դեպքում։ Գազի բալոնը տաքացնելուց և դրա մեջ ճնշումը չափելուց հետո պարզվել է, որ այն 1,5 մթնոլորտ է։ Որքա՞ն է տաքանալուց հետո գազի ջերմաստիճանը բալոնում: Որքա՞ն է փոխվել գազի ներքին էներգիան, եթե օդապարիկում 4 մոլ ազոտ է եղել։

Առաջին հարցին պատասխանելու համար օգտագործում ենք հետևյալ արտահայտությունը՝

P₁ / T₁=P₂ / T _2.

Որտեղից մենք ստանում ենք՝

T₂=P₂ / P₁ T _1.

Այս արտահայտության մեջ ճնշումը կարող է փոխարինվել կամայական միավորներովչափումները, քանի որ դրանք նվազում են, և ջերմաստիճանը միայն կելվիններով է: Դրանով մենք ստանում ենք՝

T_{2=1,5 /1298,15=447,224 Կ.}

Հաշվարկված ջերմաստիճանը Ցելսիուսի աստիճանով 174 °C է։

Քանի որ ազոտի մոլեկուլը երկատոմիկ է, տաքացման ընթացքում նրա ներքին էներգիայի փոփոխությունը կարող է որոշվել հետևյալ կերպ՝

ΔU=5 / 2nRΔT.

Փոխարինելով հայտնի արժեքները այս արտահայտության մեջ՝ մենք կստանանք խնդրի երկրորդ հարցի պատասխանը՝ ΔU=+12,4 կՋ։