Ինչպես գիտեք, ցանկացած ֆիզիկական մեծություն պատկանում է երկու տեսակներից մեկին, այն կա՛մ սկալյար է, կա՛մ վեկտոր: Այս հոդվածում մենք կդիտարկենք այնպիսի կինեմատիկական բնութագրեր, ինչպիսիք են արագությունը և արագացումը, ինչպես նաև ցույց կտանք, թե ուր են ուղղված արագացման և արագության վեկտորները:
Ի՞նչ է արագությունը և արագացումը:
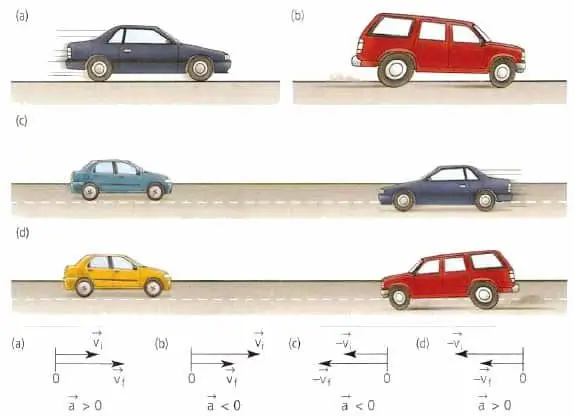
Այս պարբերությունում նշված երկու մեծություններն էլ կարևոր բնութագրիչներ են ցանկացած տեսակի շարժման համար, անկախ նրանից՝ այն շարժում է մարմինը ուղիղ գծով, թե կոր ճանապարհով:
Արագությունը այն արագությունն է, որով կոորդինատները փոխվում են ժամանակի ընթացքում: Մաթեմատիկորեն այս արժեքը հավասար է անցած տարածության ժամանակային ածանցյալին, այսինքն՝
v¯=dl¯/dt.
Այստեղ l¯ վեկտորն ուղղված է ուղու սկզբնական կետից մինչև վերջակետ:
Իր հերթին, արագացումը այն արագությունն է, որով արագությունը ինքնին փոխվում է ժամանակի ընթացքում: Բանաձևի տեսքով կարելի է գրել այսպես՝
a¯=dv¯/dt.
Ակնհայտ է, որ վերցնելով երկրորդ ածանցյալըl¯ տեղաշարժի վեկտորը ժամանակի ընթացքում կստանանք նաև արագացման արժեքը:
Քանի որ արագությունը չափվում է վայրկյանում մետրերով, արագացումը, գրավոր արտահայտության համաձայն, չափվում է մետր վայրկյանում քառակուսի։

Որտե՞ղ են արագացման և արագության վեկտորները:
Ֆիզիկայի մեջ մարմնի ցանկացած մեխանիկական շարժում սովորաբար բնութագրվում է որոշակի հետագծով: Վերջինս ինչ-որ երևակայական կոր է, որով մարմինը շարժվում է տարածության մեջ։ Օրինակ՝ ուղիղ գիծը կամ շրջանագիծը ընդհանուր շարժման ուղիների պարզ օրինակներ են։
Մարմնի արագության վեկտորը միշտ ուղղված է շարժման ուղղությամբ՝ անկախ նրանից՝ մարմինը դանդաղում է, թե արագանում, շարժվում է ուղիղ գծով, թե կորի երկայնքով։ Եթե խոսենք երկրաչափական առումով, ապա արագության վեկտորը շոշափելիորեն ուղղված է այն հետագծի այն կետին, որտեղ ներկայումս գտնվում է մարմինը:
Նյութի կամ մարմնի կետի արագացման վեկտորը կապ չունի արագության հետ: Այս վեկտորն ուղղված է արագության փոփոխության ուղղությամբ։ Օրինակ, ուղղագիծ շարժման համար a¯ արժեքը կարող է կամ համընկնել v¯-ի ուղղությամբ կամ հակառակ լինել v¯-ին:
Մարմնի վրա գործող ուժ և արագացում
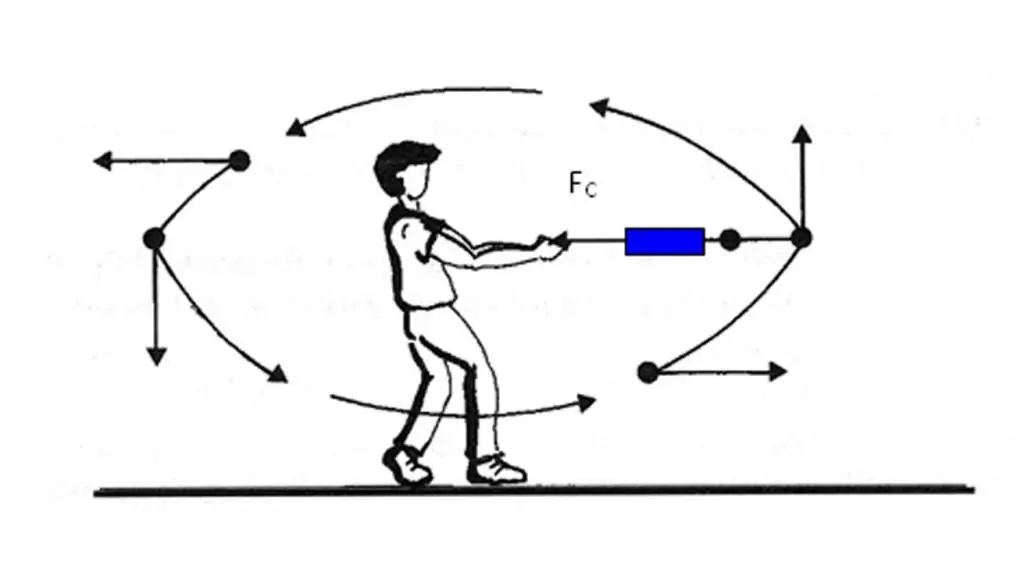
Մենք պարզել ենք, որ մարմնի արագացման վեկտորն ուղղված է արագության վեկտորի փոփոխությանը։ Այնուամենայնիվ, միշտ չէ, որ հեշտ է որոշել, թե ինչպես է արագությունը փոխվում հետագծի տվյալ կետում: Ավելին, արագության փոփոխությունը որոշելու համար անհրաժեշտ է կատարել գործողությունըվեկտորային տարբերություններ. a¯ վեկտորի ուղղությունը որոշելիս այս դժվարություններից խուսափելու համար արագ պարզելու մեկ այլ միջոց կա:
Ստորև ներկայացնում ենք Նյուտոնի հայտնի և հայտնի օրենքը յուրաքանչյուր ուսանողի համար.
F¯=ma¯.
Բանաձևը ցույց է տալիս, որ մարմիններում արագացման պատճառը դրանց վրա ազդող ուժն է։ Քանի որ m զանգվածը սկալյար է, ուժի վեկտորը F¯ և արագացման վեկտորը a¯ նույն ուղղությամբ են: Այս փաստը պետք է հիշել և կիրառել գործնականում ամեն անգամ, երբ անհրաժեշտություն կա որոշելու մեծության ուղղությունը a¯:
Եթե մարմնի վրա գործում են մի քանի տարբեր ուժեր, ապա արագացման վեկտորի ուղղությունը հավասար կլինի բոլոր ուժերի առաջացող վեկտորին:
Շրջանաձև շարժում և արագացում
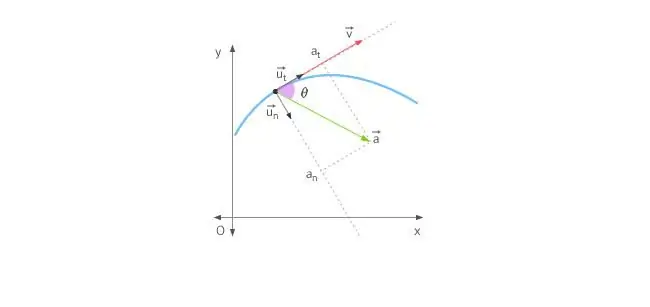
Երբ մարմինը շարժվում է ուղիղ գծով, արագացումն ուղղված է առաջ կամ հետ: Շրջանակով շարժման դեպքում իրավիճակը բարդանում է նրանով, որ արագության վեկտորն անընդհատ փոխում է իր ուղղությունը։ Հաշվի առնելով վերը նշվածը, ընդհանուր արագացումը որոշվում է իր երկու բաղադրիչներով՝ շոշափելի և նորմալ արագացումներով:
Տանգենցիալ արագացումն ուղղված է ճիշտ այնպես, ինչպես արագության վեկտորը կամ դրա դեմ: Այլ կերպ ասած, այս արագացման բաղադրիչն ուղղված է հետագծի շոշափողի երկայնքով: Շոշափող արագացումը նկարագրում է ինքնին արագության մոդուլի փոփոխությունը:
Նորմալ արագացումն ուղղվում է նորմալի երկայնքով դեպի հետագծի տվյալ կետը՝ հաշվի առնելով դրա կորությունը։ Շրջանաձև շարժման դեպքում այս բաղադրիչի վեկտորը ցույց է տալիսդեպի կենտրոն, այսինքն՝ նորմալ արագացումն ուղղված է պտտման շառավղով։ Այս բաղադրիչը հաճախ կոչվում է կենտրոնաձիգ:
Լրիվ արագացումը այս բաղադրիչների գումարն է, ուստի նրա վեկտորը կարող է կամայականորեն ուղղորդվել շրջանագծի նկատմամբ:
Եթե մարմինը պտտվում է առանց գծային արագությունը փոխելու, ապա գոյություն ունի միայն զրոյական նորմալ բաղադրիչ, ուստի ամբողջ արագացման վեկտորն ուղղված է շրջանագծի կենտրոնին: Նշենք, որ այս կենտրոնի վրա նույնպես ազդում է մի ուժ, որը մարմինը պահում է իր հետագծի վրա: Օրինակ՝ Արեգակի գրավիտացիոն ուժը մեր Երկիրը և մյուս մոլորակները պահում են իրենց ուղեծրերում։






