Մեծ միասնական տեսությունը (GUT, GUT կամ GUT - բոլոր երեք հապավումները կօգտագործվեն հոդվածում) մասնիկների ֆիզիկայի մոդել է, որտեղ բարձր էներգիայի դեպքում ստանդարտ մոդելի երեք չափիչ փոխազդեցությունները, որոնք որոշում են էլեկտրամագնիսականը:, թույլ և ուժեղ փոխազդեցությունները կամ ուժերը միավորվում են մեկ ուժի մեջ: Այս համակցված փոխազդեցությունը բնութագրվում է ավելի մեծ չափման մեկ սիմետրիկությամբ, հետևաբար մի քանի կրող ուժերով, բայց մեկ մշտական կապով: Եթե բնության մեջ տեղի է ունենում մեծ միավորում, ապա վաղ տիեզերքում մեծ միավորման դարաշրջանի հավանականություն կա, որտեղ հիմնարար ուժերը դեռ տարբեր չեն:
Մեծ միասնական տեսություն համառոտ
Մոդելները, որոնք չեն միավորում բոլոր փոխազդեցությունները՝ օգտագործելով մեկ պարզ խումբ որպես չափիչի համաչափություն, դա անում են կիսահասարակ խմբերի միջոցով, կարող են դրսևորել նմանատիպ հատկություններ և երբեմն կոչվում են նաև մեծ միավորման տեսություններ:
Ձգողականությունը մյուս երեք ուժերի հետ համատեղելը կապահովի ամեն ինչի տեսություն (OO), այլ ոչ թե GUT: Այնուամենայնիվ, GUT հաճախ դիտվում է որպես միջանկյալ քայլ դեպի OO: Սրանք բոլորը բնորոշ գաղափարներ են միավորման և գերմիավորման մեծ տեսությունների համար:
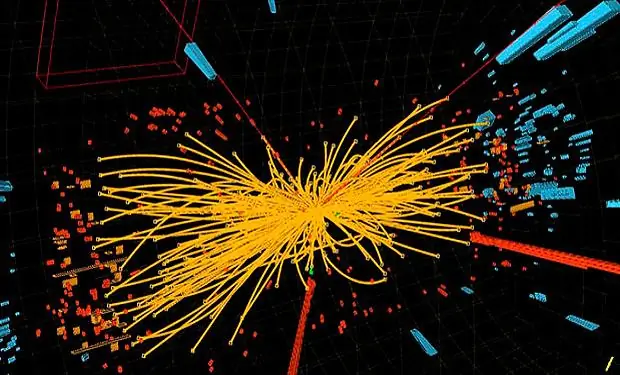
Նոր մասնիկները, որոնք կանխատեսվել են GUT մոդելների կողմից, ակնկալվում է, որ զանգվածներ կունենան GUT սանդղակի շուրջ՝ ընդամենը մի քանի կարգով Պլանկի սանդղակից ցածր, և, հետևաբար, անհասանելի են ցանկացած առաջարկվող մասնիկների բախման փորձերի համար: Հետևաբար, GUT մոդելների կողմից կանխատեսված մասնիկները չեն կարող ուղղակիորեն դիտարկվել, և փոխարենը, մեծ միավորման էֆեկտները կարող են հայտնաբերվել անուղղակի դիտարկումների միջոցով, ինչպիսիք են պրոտոնի քայքայումը, տարրական մասնիկների էլեկտրական դիպոլային մոմենտները կամ նեյտրինոյի հատկությունները: Որոշ աղիքներ, ինչպիսիք են Pati Salam մոդելը, կանխատեսում են մագնիսական մոնոպոլների գոյությունը:
Մոդելների բնութագրերը
GUT մոդելները, որոնց նպատակը լիովին իրատեսական լինելն է, բավականին բարդ են նույնիսկ ստանդարտ մոդելի համեմատ, քանի որ դրանք պետք է ներմուծեն լրացուցիչ դաշտեր և փոխազդեցություններ կամ նույնիսկ տարածության լրացուցիչ չափումներ: Այս բարդության հիմնական պատճառը կայանում է նրանում, որ դիտարկված ֆերմիոնային զանգվածները վերարտադրելու և խառնվող անկյունների դժվարությունն է, ինչը կարող է պայմանավորված լինել GUT-ի ավանդական մոդելներից դուրս որոշ լրացուցիչ ընտանեկան սիմետրիաների առկայությամբ: Այս դժվարության և որևէ նկատելի մեծ միավորման էֆեկտի բացակայության պատճառով դեռևս գոյություն չունի ընդհանուր ընդունված GUT մոդել:

Պատմականորեն առաջինըիսկական GUT հիմնված Լիի պարզ SU խմբի վրա, առաջարկվել է Հովարդ Ջորջի և Շելդոն Գլաշուի կողմից 1974 թվականին: Գեորգի-Գլաշոու մոդելին նախորդել է կիսահասարակ Lie հանրահաշվի Փաթի-Սալամ մոդելը, որն առաջարկվել է Աբդուս Սալամի և Ջոգեշ Պատիի կողմից, ովքեր առաջինն առաջարկել են միավորող չափիչ փոխազդեցությունները::
Անվան պատմություն
GUT (GUT) հապավումը առաջին անգամ ստեղծվել է 1978 թվականին CERN-ի հետազոտողներ Ջոն Էլլիսի, Անջեյ Բուրասի, Մերի Ք. Նույն տարում Նանոպուլոսն առաջինն էր, ով օգտագործեց հապավումը հոդվածում։ Մի խոսքով, մեծ աշխատանք է կատարվել Մեծ միասնական տեսության ճանապարհին։

Հասկացությունների ընդհանրություն
SU հապավումը օգտագործվում է մեծ միավորման տեսություններին մատնանշելու համար, որոնց հաճախակի կանդրադառնանք այս հոդվածում: Այն փաստը, որ էլեկտրոնների և պրոտոնների էլեկտրական լիցքերը, կարծես, ծայրահեղ ճշգրտությամբ ջնջում են միմյանց, կարևոր է մեզ հայտնի մակրոսկոպիկ աշխարհի համար, սակայն տարրական մասնիկների այս կարևոր հատկությունը բացատրված չէ մասնիկների ֆիզիկայի ստանդարտ մոդելում: Թեև Ստանդարտ մոդելում ուժեղ և թույլ փոխազդեցությունների նկարագրությունը հիմնված է չափիչի սիմետրիաների վրա, որոնք կառավարվում են պարզ SU(3) և SU(2) սիմետրիկ խմբերով, որոնք թույլ են տալիս միայն դիսկրետ լիցքեր, մնացած բաղադրիչը՝ թույլ հիպերլիցքավորման փոխազդեցությունը, նկարագրված է. Աբելյան U(1), որը սկզբունքորեն թույլ է տալիսԳանձումների կամայական բաշխում։

Դիտարկված լիցքի քվանտացումը, մասնավորապես այն փաստը, որ բոլոր հայտնի տարրական մասնիկները կրում են էլեկտրական լիցքեր, որոնք կարծես տարրական լիցքի ⅓-ի ճշգրիտ բազմապատիկ են, հանգեցրեց այն մտքին, որ հիպերլիցքների փոխազդեցությունները և, հնարավոր է, ուժեղ և թույլ փոխազդեցությունները կարող են ստեղծվել: մեկ մեծ միասնական փոխազդեցության մեջ, որը նկարագրված է մեկ ավելի մեծ պարզ սիմետրիկ խմբի կողմից, որը պարունակում է ստանդարտ մոդել: Սա ինքնաբերաբար կկանխատեսի տարրական մասնիկների բոլոր լիցքերի քվանտացված բնույթը և արժեքները: Քանի որ դա նաև հանգեցնում է մեր դիտարկած հիմքում ընկած փոխազդեցությունների հարաբերական ուժեղությունների կանխատեսմանը, մասնավորապես թույլ խառնման անկյունին, Grand Unification-ը իդեալականորեն նվազեցնում է անկախ մուտքերի քանակը, բայց նաև սահմանափակվում է դիտարկումներով: Որքան էլ համընդհանուր թվա մեծ միասնական տեսությունը, դրա վերաբերյալ գրքերն այնքան էլ տարածված չեն:
Ջորջի-Գլազգո տեսություն (SU (5))
Մեծ միավորումը հիշեցնում է էլեկտրական և մագնիսական ուժերի միավորումը 19-րդ դարում Մաքսվելի էլեկտրամագնիսականության տեսության մեջ, սակայն դրա ֆիզիկական իմաստը և մաթեմատիկական կառուցվածքը որակապես տարբեր են:
Սակայն ակնհայտ չէ, որ ընդլայնված մեծ միասնական համաչափության համար ամենապարզ հնարավոր ընտրությունը տարրական մասնիկների ճիշտ բազմություն արտադրելն է: Այն փաստը, որ ներկայումս հայտնի նյութի բոլոր մասնիկները լավ տեղավորվում են SU(5) խմբի ներկայացման երեք ամենափոքր տեսությունների մեջ և անմիջապես կրում են ճիշտ դիտարկելի լիցքերը, առաջիններից մեկն է ևԱմենակարևոր պատճառները, թե ինչու մարդիկ հավատում են, որ մեծ միասնական տեսությունը կարող է իրականում իրականանալ բնության մեջ:

SU(5)-ի երկու ամենափոքր անկրճատելի ներկայացումները 5-ն են և 10-ը: Ստանդարտ նշումով 5-ը պարունակում է աջակողմյան ներքև տիպի գունային եռյակի և ձախակողմյան իզոսպինի կրկնակի լիցքի միավորներ, մինչդեռ 10-ը: պարունակում է վեր տիպի քվարկի վեց բաղադրիչ, գունավորում է ձախակողմյան տիպի քվարկի և աջակողմյան էլեկտրոնի եռյակը: Այս սխեման պետք է վերարտադրվի նյութի երեք հայտնի սերունդներից յուրաքանչյուրի համար: Հատկանշական է, որ տեսությունը այս բովանդակությամբ անոմալիաներ չի պարունակում։
Հիպոթետիկ աջակողմյան նեյտրինոները SU(5) սինգլ են, ինչը նշանակում է, որ դրա զանգվածը արգելված չէ որևէ համաչափությամբ. նրան պետք չէ ինքնաբերաբար խախտել համաչափությունը, ինչը բացատրում է, թե ինչու է նրա զանգվածը մեծ լինելու։
Այստեղ նյութի միավորումն ավելի ամբողջական է, քանի որ անկրճատելի սպինորի 16 ներկայացումը պարունակում է SU(5) և 5-ը և 10-ը և աջակողմյան նեյտրինոները, և, հետևաբար, մեկ սերնդի մասնիկների ընդհանուր պարունակությունը: ընդլայնված ստանդարտ մոդել նեյտրինո զանգվածներով: Սա արդեն ամենամեծ պարզ խումբն է, որը հասնում է նյութի միավորմանը մի սխեմայի մեջ, որը ներառում է միայն նյութի արդեն հայտնի մասնիկներ (բացառությամբ Հիգսի հատվածի):
Քանի որ տարբեր ստանդարտ մոդելների ֆերմիոնները խմբավորված են ավելի մեծ պատկերների մեջ, GUT-ները հատուկ կանխատեսում են փոխհարաբերությունները ֆերմիոնների զանգվածների միջև, օրինակ՝ էլեկտրոնի ևներքև քվարկ, մյուոն և տարօրինակ քվարկ, և տաու լեպտոն և ներքև քվարկ՝ SU(5): Այս զանգվածային գործակիցներից ոմանք մոտավոր են, բայց շատերը՝ ոչ։

SO(10) տեսություն
SO(10)-ի բոզոնային մատրիցը գտնում ենք՝ վերցնելով SU(5) 10 + 5 ներկայացման 15×15 մատրիցը և ավելացնելով աջ նեյտրինոյի լրացուցիչ տող և սյունակ: Բոզոնները կարելի է գտնել՝ ավելացնելով գործընկեր 20 լիցքավորված բոզոններից յուրաքանչյուրին (2 աջ W բոզոն, 6 զանգվածային լիցքավորված գլյուոն և 12 X/Y տիպի բոզոն) և ավելացնելով լրացուցիչ ծանր չեզոք Z բոզոն՝ 5 չեզոք բոզոններ ստանալու համար։ Բոզոնային մատրիցը յուրաքանչյուր տողում և սյունակում կունենա բոզոն կամ իր նոր գործընկեր: Այս զույգերը միավորվում են՝ ստեղծելով ծանոթ 16D Dirac պտտվող մատրիցներ SO(10).
Ստանդարտ մոդել
Ստանդարտ մոդելի ոչ քիրալային ընդարձակումները՝ տրոհված բազմակի մասնիկների վեկտորային սպեկտրով, որոնք բնականաբար հայտնվում են ավելի բարձր SU(N) GUT-ներում, զգալիորեն փոխում են անապատի ֆիզիկան և հանգեցնում են սովորական երեք քվարկ-լեպտոնի իրատեսական (շարային մասշտաբի) մեծ միավորմանը: ընտանիքներ նույնիսկ առանց սուպերսիմետրիա օգտագործելու (տես ստորև): Մյուս կողմից, սուպերսիմետրիկ SU(8) GUT-ում առաջացող նոր բացակայող VEV մեխանիզմի ի հայտ գալու պատճառով, կարելի է գտնել չափիչի հիերարխիայի խնդրի միաժամանակյա լուծում (կրկնակի-եռյակի բաժանում) և համի միավորման խնդիրը:
Այլ տեսություններ և տարրական մասնիկներ
GUT չորս ընտանիքներով/սերունդներով, SU(8). ենթադրելով, որ ֆերմիոնների 4 սերունդները 3-ի փոխարեն առաջացնում են ընդհանուր 64 տեսակի մասնիկներ: Նրանք կարող են տեղադրվել 64=8 + 56 SU(8) ներկայացուցչություններում: Սա կարելի է բաժանել SU(5) × SU(3) F × U(1), որը SU(5) տեսությունն է, ինչպես նաև մի քանի ծանր բոզոններ, որոնք ազդում են սերնդի թվի վրա:
GUT չորս ընտանիքներով/սերունդներով, O(16). Կրկին, ենթադրելով ֆերմիոնների 4 սերունդ, 128 մասնիկներ և հակամասնիկներ կարող են տեղավորվել մեկ O(16) սպինորի ներկայացման մեջ: Այս բոլոր բաները հայտնաբերվեցին մեծ միասնական տեսության ճանապարհին:






