Վիճակագրական համակարգերում տեղի ունեցող գործընթացների ուսումնասիրությունը բարդանում է մասնիկների նվազագույն չափերով և դրանց հսկայական քանակով: Գործնականում անհնար է յուրաքանչյուր մասնիկ առանձին դիտարկել, հետևաբար, ներկայացվում են վիճակագրական մեծություններ՝ մասնիկների միջին արագությունը, դրանց կոնցենտրացիան, մասնիկների զանգվածը։ Համակարգի վիճակը բնութագրող բանաձևը՝ հաշվի առնելով մանրադիտակային պարամետրերը, կոչվում է գազերի մոլեկուլային-կինետիկ տեսության հիմնական հավասարում (MKT):
Մի փոքր մասնիկների միջին արագության մասին
Մասնիկների արագության որոշումն առաջին անգամ իրականացվել է փորձարարական եղանակով։ Դպրոցական ուսումնական ծրագրից հայտնի փորձը, որն անցկացրել է Օտտո Սթերնը, հնարավորություն է տվել պատկերացում կազմել մասնիկների արագության մասին: Փորձի ընթացքում ուսումնասիրվել է արծաթի ատոմների շարժումը պտտվող բալոններում՝ սկզբում տեղակայման անշարժ վիճակում, այնուհետև երբ այն պտտվում է որոշակի անկյունային արագությամբ։
Արդյունքում պարզվել է, որ արծաթի մոլեկուլների արագությունը գերազանցում է ձայնի արագությունը և կազմում է 500 մ/վ։ Փաստը բավականին հետաքրքիր է, քանի որ մարդու համար դժվար է զգալ նյութերի մեջ մասնիկների շարժման նման արագություն։
Իդեալական գազ
Շարունակեք հետազոտությունըԴա հնարավոր է թվում միայն մի համակարգում, որի պարամետրերը կարող են որոշվել ուղղակի չափումների միջոցով՝ օգտագործելով ֆիզիկական գործիքներ: Արագությունը չափվում է արագաչափով, բայց մեկ մասնիկին արագաչափ կցելու գաղափարն անհեթեթ է։ Միայն մասնիկների շարժման հետ կապված մակրոսկոպիկ պարամետրը կարող է ուղղակիորեն չափվել:
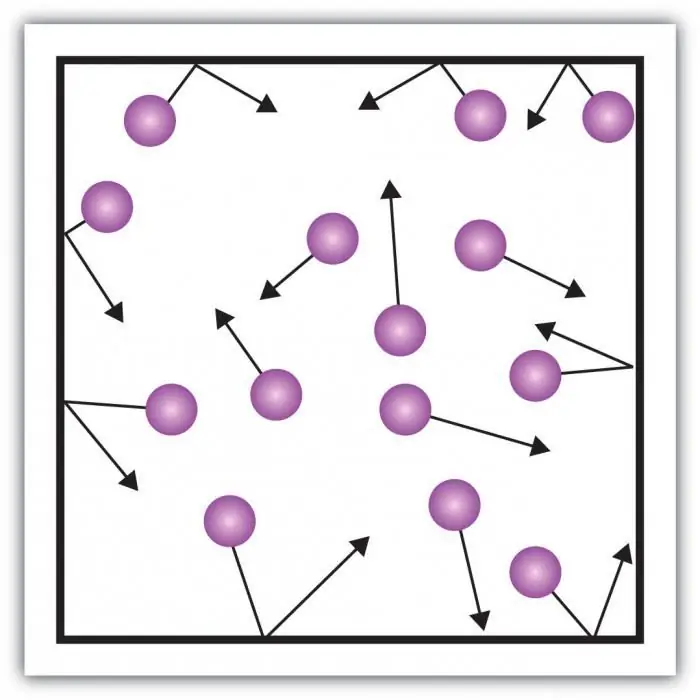
Հաշվի առեք գազի ճնշումը: Անոթի պատերի վրա ճնշումը ստեղծվում է անոթի գազի մոլեկուլների ազդեցությունից: Նյութի գազային վիճակի առանձնահատկությունը մասնիկների միջև բավական մեծ հեռավորությունների և միմյանց հետ փոքր փոխազդեցության մեջ է։ Սա թույլ է տալիս ուղղակիորեն չափել դրա ճնշումը։
Փոխազդող մարմինների ցանկացած համակարգ բնութագրվում է պոտենցիալ էներգիայով և շարժման կինետիկ էներգիայով: Իրական գազը բարդ համակարգ է։ Պոտենցիալ էներգիայի փոփոխականությունը համակարգվածության չի տալիս: Խնդիրը կարող է լուծվել գազի բնորոշ հատկությունները կրող մոդելի ներդրմամբ՝ մի կողմ թողնելով փոխազդեցության բարդությունը։
Իդեալական գազը նյութի վիճակ է, որի դեպքում մասնիկների փոխազդեցությունը աննշան է, փոխազդեցության պոտենցիալ էներգիան ձգտում է զրոյի: Նշանակալի կարելի է համարել միայն շարժման էներգիան, որը կախված է մասնիկների արագությունից։
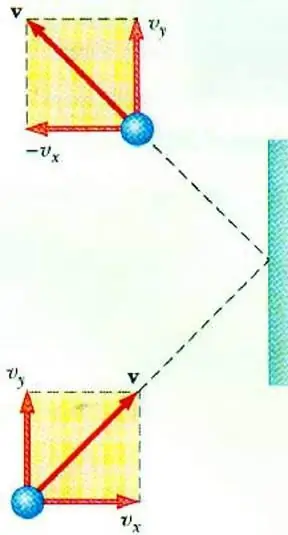
Գազի իդեալական ճնշում
Գազի ճնշման և նրա մասնիկների արագության միջև կապը բացահայտելու համար թույլ է տալիս իդեալական գազի MKT-ի հիմնական հավասարումը: Անոթի մեջ շարժվող մասնիկը պատին բախվելիս նրան փոխանցում է իմպուլս, որի արժեքը կարելի է որոշել երկրորդ օրենքի հիման վրա. Նյուտոն:
F∆t=2m0vx
Առաձգական ազդեցության ժամանակ մասնիկի իմպուլսի փոփոխությունը կապված է նրա արագության հորիզոնական բաղադրիչի փոփոխության հետ։ F-ն այն ուժն է, որը գործում է մասնիկի կողմից պատի վրա կարճ ժամանակով t; m0 - մասնիկների զանգված։
Գազի բոլոր մասնիկները ∆t ժամանակի ընթացքում բախվում են S տարածքի մակերեսին, շարժվելով մակերեսի ուղղությամբ vx արագությամբ և գտնվում են Sυ ծավալով բալոնում: x Δt. Մասնիկների n կոնցենտրացիայի դեպքում մոլեկուլների ուղիղ կեսը շարժվում է դեպի պատը, մյուս կեսը շարժվում է հակառակ ուղղությամբ։
Հաշվի առնելով բոլոր մասնիկների բախումը, մենք կարող ենք գրել Նյուտոնի օրենքը տարածքի վրա ազդող ուժի համար:
F∆t=nm0vx2S∆t
Քանի որ գազի ճնշումը սահմանվում է որպես մակերևույթին ուղղահայաց գործող ուժի հարաբերակցություն վերջինիս մակերեսին, մենք կարող ենք գրել՝
p=F: S=nm0vx2
Ստացված հարաբերությունը որպես MKT-ի հիմնական հավասարում չի կարող նկարագրել ամբողջ համակարգը, քանի որ դիտարկվում է շարժման միայն մեկ ուղղություն:
Մաքսվելի բաշխում
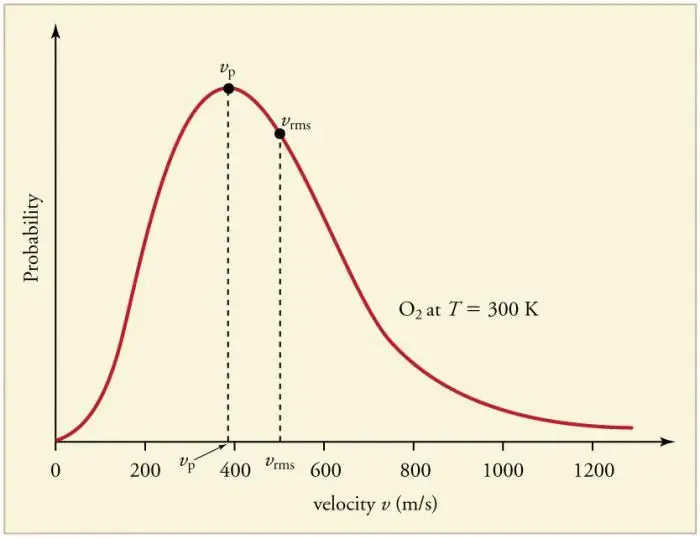
Գազի մասնիկների շարունակական հաճախակի բախումները պատերի և միմյանց հետ հանգեցնում են արագությունների (էներգիաների) մասով մասնիկների որոշակի վիճակագրական բաշխման հաստատմանը։ Բոլոր արագության վեկտորների ուղղությունները հավասարապես հավանական են: Այս բաշխումը կոչվում է Մաքսվելի բաշխում։ 1860 թվականին այս օրինաչափությունն էրստացված J. Maxwell-ի կողմից MKT-ի հիման վրա: Բաշխման օրենքի հիմնական պարամետրերը կոչվում են արագություններ՝ հավանական, որը համապատասխանում է կորի առավելագույն արժեքին, և արմատ-միջին քառակուսի vkv=√‹v2 › - մասնիկների արագության միջին քառակուսին:
Գազի ջերմաստիճանի բարձրացումը համապատասխանում է արագության բարձրացմանը։
Ելնելով այն փաստից, որ բոլոր արագությունները հավասար են, և դրանց մոդուլներն ունեն նույն արժեքը, մենք կարող ենք ենթադրել.
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, սկսած՝ ‹ vx2›=‹v2›: 3›
MKT-ի հիմնական հավասարումը, հաշվի առնելով գազի ճնշման միջին արժեքը, հետևյալն է՝
p=nm0‹v2›: 3.
Այս հարաբերությունը եզակի է նրանով, որ որոշում է կապը մանրադիտակային պարամետրերի միջև՝ արագություն, մասնիկների զանգված, մասնիկների կոնցենտրացիան և ընդհանուր առմամբ գազի ճնշումը:
Օգտագործելով մասնիկների կինետիկ էներգիայի հայեցակարգը, MKT-ի հիմնական հավասարումը կարելի է այլ կերպ վերաշարադրել.
p=2nm0‹v2›: 6=2n‹Ek›: 3
Գազի ճնշումը համամասնական է նրա մասնիկների կինետիկ էներգիայի միջին արժեքին։
Ջերմաստիճան
Հետաքրքիր է, որ փակ անոթում գազի մշտական քանակի համար կարելի է կապել գազի ճնշումը և մասնիկների շարժման էներգիայի միջին արժեքը: Այս դեպքում ճնշումը կարող է չափվել էներգիայի չափման միջոցովմասնիկներ.
Ինչ անել? Ի՞նչ արժեք կարելի է համեմատել կինետիկ էներգիայի հետ: Ջերմաստիճանը, պարզվում է, այդպիսի արժեք է։

Ջերմաստիճանը նյութերի ջերմային վիճակի չափումն է։ Չափելու համար օգտագործվում է ջերմաչափ, որի հիմքը տաքացնելիս աշխատող հեղուկի (ալկոհոլ, սնդիկ) ջերմային ընդարձակումն է։ Ջերմաչափի սանդղակը ստեղծվում է փորձարարական եղանակով։ Սովորաբար դրա վրա դրվում են հետքեր, որոնք համապատասխանում են աշխատանքային հեղուկի դիրքին մշտական ջերմային վիճակում տեղի ունեցող որոշակի ֆիզիկական գործընթացի ժամանակ (եռացող ջուր, հալվող սառույց): Տարբեր ջերմաչափերն ունեն տարբեր մասշտաբներ: Օրինակ՝ Ցելսիուս, Ֆարենհայթ։

Ջերմաստիճանի համընդհանուր սանդղակ
Գազի ջերմաչափերը կարելի է ավելի հետաքրքիր համարել աշխատանքային հեղուկի հատկություններից անկախ լինելու առումով։ Նրանց մասշտաբները կախված չեն օգտագործվող գազի տեսակից: Նման սարքում հիպոթետիկորեն կարելի է առանձնացնել այն ջերմաստիճանը, որի դեպքում գազի ճնշումը ձգտում է զրոյի: Հաշվարկները ցույց են տալիս, որ այս արժեքը համապատասխանում է -273,15 oC: Ջերմաստիճանի սանդղակը (բացարձակ ջերմաստիճանի սանդղակ կամ Կելվինի սանդղակ) ներդրվել է 1848 թվականին։ Որպես այս սանդղակի հիմնական կետ ընդունվել է գազի զրոյական ճնշման հնարավոր ջերմաստիճանը։ Սանդղակի միավոր հատվածը հավասար է Ցելսիուսի սանդղակի միավոր արժեքին: Գազային գործընթացներն ուսումնասիրելիս ավելի հարմար է թվում MKT հիմնական հավասարումը գրելը ջերմաստիճանի միջոցով:
Ճնշման և ջերմաստիճանի կապը
Էմպիրիկորեն, դուք կարող եք դա հաստատելգազի ճնշման համաչափությունը նրա ջերմաստիճանին. Միևնույն ժամանակ պարզվել է, որ ճնշումն ուղիղ համեմատական է մասնիկների կոնցենտրացիայիը՝
P=nkT,
որտեղ T-ը բացարձակ ջերմաստիճան է, k-ն հաստատուն է, որը հավասար է 1,38•10-23J/K.
Հիմնական արժեքը, որն ունի հաստատուն արժեք բոլոր գազերի համար, կոչվում է Բոլցմանի հաստատուն:
Համեմատելով ճնշման կախվածությունը ջերմաստիճանից և MKT գազերի հիմնական հավասարումից՝ կարող ենք գրել.
‹Ek›=3kT: 2
Գազի մոլեկուլների շարժման կինետիկ էներգիայի միջին արժեքը համաչափ է նրա ջերմաստիճանին։ Այսինքն՝ ջերմաստիճանը կարող է ծառայել որպես մասնիկների շարժման կինետիկ էներգիայի չափ։






