Բուրգը պրիզմայի հետ միասին կատարյալ բազմանիստ է եռաչափ տարածության մեջ, դրանց երկրաչափական բնութագրերը ուսումնասիրվում են ավագ դպրոցում։ Այս հոդվածում մենք կքննարկենք, թե ինչ են բուրգերը, ինչ տարրերից են դրանք բաղկացած, ինչպես նաև հակիրճ կբնութագրենք ճիշտ բուրգերը:
Երկրաչափական պատկերի բուրգ
Երկրաչափության տեսակետից բուրգը տարածական պատկեր է՝ բաղկացած մեկ բազմանկյունից և մի քանի եռանկյունից։ Այս ցուցանիշը ստանալը բավականին պարզ է. Դա անելու համար վերցնում ենք n կողմերով բազմանկյուն, այնուհետև տարածության մեջ ընտրում ենք կամայական կետ, որը չի ընկած բազմանկյունի հարթության մեջ և միացնում ենք բազմանկյան յուրաքանչյուր գագաթ այս կետին: Ակնհայտ է, որ այս ձևով ձևավորված պատկերը կունենա n եռանկյուն, որոնք միմյանց հետ կապված են մեկ գագաթով:
Նկարագրված պատկերի երկրաչափական ձևը պատկերացնելու համար եկեք նկարենք։

Սա ցույց է տալիս քառանկյուն բուրգ, որի հիմքն էքառանկյուն, իսկ կողային մակերեսը կազմված է չորս եռանկյուններով, որոնք ունեն ընդհանուր գագաթ:
Բուրգի տարրեր
Ինչպես ցանկացած բազմանիստ, բուրգը ձևավորվում է երեք տեսակի տարրերով.
- եզրեր;
- գագաթներ;
- կողիկներ.
Դեմքերը հարթությունների մասեր են, որոնք առանձնացնում են պատկերի ներքին ծավալը շրջապատող տարածությունից: Եթե բուրգի հիմքը պարունակում է n-գոն, ապա նրա երեսների թիվը միշտ n+1 է։ Դրանցից n կողմերը եռանկյուն են, իսկ մի կողմը նշված n-անկյունային հիմքն է։
Վերտիկները այն կետերն են, որտեղ հատվում են գործչի երեք կամ ավելի դեմքերը: Հիմքի շրջանը պարունակում է n գագաթ, որոնցից յուրաքանչյուրը կազմված է երկու եռանկյուն երեսով և հիմքով։ Այն կետը, որտեղ n եռանկյուն կողմերը հանդիպում են, կոչվում է բուրգի գագաթ։ Այսպիսով, դիտարկվող պատկերը բաղկացած է n+1 գագաթներից։
Ծայրերը ուղիղ գծեր են, որոնք առաջանում են երկու երեսների հատման ժամանակ: Յուրաքանչյուր եզր իր ծայրերում սահմանափակված է երկու գագաթներով: n-gon հիմքով ցանկացած բուրգ պարունակում է 2n եզրեր: Այս թվի կեսը, այսինքն՝ n-ը, ձևավորվում է բացառապես կողային եռանկյունների հատումից։
Թվերի հնարավոր տեսակներ
Քննարկվող պատկերի անվանումը եզակիորեն որոշվում է հիմքում ընկած բազմանկյունի տեսակով: Օրինակ, եթե այն ունի երեք անկյուն և երեք կողմ, ապա բուրգը կլինի եռանկյուն, եթե չորսը՝ քառանկյուն և այլն։
Բազմանկյունը կարող է լինել ուռուցիկ և գոգավոր, ինչպես նաև կանոնավոր և ընդհանուր տիպ: Այս ամենը նաև որոշում է բուրգի տեսքը։
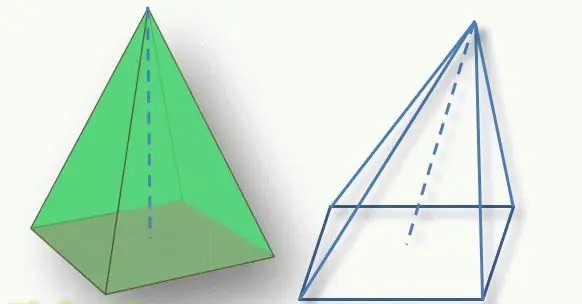
Գծապատկերի տեսակը որոշելու կարևոր կետը բուրգի գագաթի դիրքն է նրա հիմքի նկատմամբ: Վերևից մինչև բազմանկյուն հիմքը գծված ուղղահայաց հատվածը կոչվում է պատկերի բարձրություն։ Եթե այս հատվածը հատում է հիմքը իր երկրաչափական կենտրոնում (եռանկյունի համար սա միջնամասերի հատումն է, քառանկյունի համար՝ անկյունագծերի հատումը), ապա նկարը կոչվում է ուղիղ գիծ։ Հակառակ դեպքում խոսում են թեք բուրգի մասին։
Եթե հիմքի n-գոնը կանոնավոր է (հավասարակողմ եռանկյուն, քառակուսի և այլն), իսկ պատկերը՝ ուղիղ, ապա այն կոչվում է կանոնավոր բուրգ։
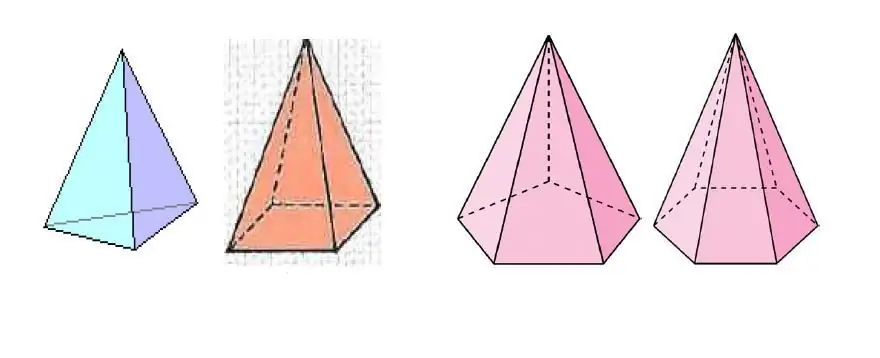
Վերևի նկարը ցույց է տալիս մի քանի բուրգեր, որոնք տարբերվում են հիմքում գտնվող բազմանկյունի կողմերի քանակով:
Կանոնավոր բուրգերի հատկությունները
Այս բուրգերը տարբերվում են այս դասի այլ պատկերներից համաչափության բարձր աստիճանով։ Այս առումով հարմար է դրանցով տարբեր երկրաչափական հաշվարկներ կատարել, օրինակ՝ ծավալը կամ մակերեսը։
Կանոնավոր բուրգը իր հիմքում պարունակում է n-գոն, որի մակերեսը եզակիորեն որոշվում է իր կողմի երկարության իմացությունից: Նկարի կողային մակերեսը կազմված է n նույնական եռանկյուններով, որոնք հավասարակողմ են։ Կողային մակերեսի վրա տեղակայված կանոնավոր բուրգի եզրերը հավասար են միմյանց: Այս եզրի երկարության արժեքը հաճախ օգտագործվում է պատկերի ապոտեմը հաշվարկելիս և մակերեսը որոշելիս:
Կանոնավոր բուրգի բարձրությունը գործչի երկրորդ կարևոր հատկանիշն է (առաջինը եզրի երկարությունն էհիմքեր): Բարձրությունը օգտագործվում է ծավալը հաշվարկելիս։
Հիմքին զուգահեռ ցանկացած հարթություն, որը հատում է բուրգի կողային երեսները, հանգեցնում է բազմանկյուն հատվածի առաջացմանը։ Այն հոմոթետիկ է հիմնական բազմանկյունի նկատմամբ։ Նկարագրված հատվածի գործողությունը հանգեցնում է նոր ֆիգուրների մի ամբողջ դասի ձևավորմանը՝ կտրված կանոնավոր բուրգեր:
Ամենահայտնի բուրգերը

Իհարկե, սրանք եգիպտական փարավոնների կանոնավոր քառանկյուն բուրգերն են։ Գիզա կոչվող վայրում կան 100-ից ավելի այս քարե հուշարձաններ, որոնց դիզայնի կատարելությունը և երկրաչափական պարամետրերի ճշգրտությունը շարունակում են զարմացնել գիտնականներին մինչ օրս։ Դրանցից ամենամեծը Քեոպսի բուրգն է, որն ունի մոտ 146 մետր բարձրություն և մոտ 230 մետր երկարություն։
Ինչ կոնկրետ ինչի են ծառայել այս բուրգերը, ինչպես նաև ինչ մեխանիզմներով և երբ են դրանք կառուցվել, մինչ օրս ոչ ոք չգիտի։






