Գազի ջերմունակությունը էներգիայի քանակությունն է, որը մարմինը կլանում է, երբ այն տաքանում է մեկ աստիճանով: Եկեք վերլուծենք այս ֆիզիկական մեծության հիմնական բնութագրերը։

Սահմանումներ
Գազի հատուկ ջերմությունը որոշակի նյութի միավոր զանգվածն է: Նրա չափման միավորներն են J/(kg·K): Ջերմության քանակությունը, որը կլանվում է մարմնի կողմից ագրեգացման վիճակի փոփոխման գործընթացում, կապված է ոչ միայն նախնական և վերջնական վիճակի, այլև անցման եղանակի հետ։

Բաժանմունք
Գազերի ջերմային հզորությունը բաժանվում է հաստատուն ծավալով որոշված արժեքի վրա (Cv), հաստատուն ճնշման (Cр)::
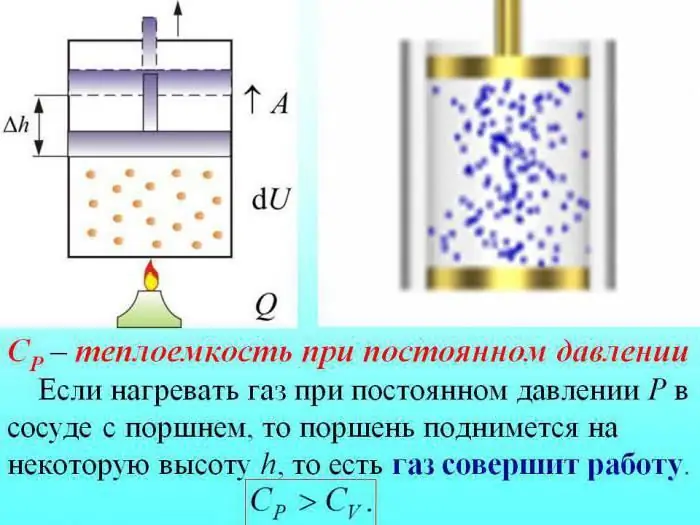
Առանց ճնշումը փոխելու տաքացման դեպքում որոշակի ջերմություն ծախսվում է գազի ընդլայնման աշխատանք առաջացնելու համար, իսկ էներգիայի մի մասը ծախսվում է ներքին էներգիան ավելացնելու համար։
Գազերի ջերմային հզորությունը մշտական ճնշման դեպքում որոշվում է ջերմության քանակով, որը ծախսվում է ներքին էներգիայի ավելացման վրա:
Գազային վիճակ. առանձնահատկություններ, նկարագրություն
Իդեալական գազի ջերմունակությունը որոշվում է հաշվի առնելով այն փաստը, որ Сp-Сv=R. Վերջին մեծությունը կոչվում է գազի համընդհանուր հաստատուն։ Դրա արժեքը համապատասխանում է 8,314 Ջ/(մոլ Կ):
Ջերմային հզորության տեսական հաշվարկներ կատարելիս, օրինակ՝ ջերմաստիճանի հետ կապը նկարագրելիս, բավարար չէ միայն թերմոդինամիկական մեթոդների կիրառումը, կարևոր է զինվել ստատիկ ֆիզիկայի տարրերով։
Գազերի ջերմունակությունը ներառում է որոշ մոլեկուլների փոխադրական շարժման էներգիայի միջին արժեքի հաշվարկը։ Նման շարժումն ամփոփվում է մոլեկուլի պտտվող և թարգմանական շարժումից, ինչպես նաև ատոմների ներքին թրթռումներից։
Ստատիկ ֆիզիկայում տեղեկություն կա, որ պտտման և փոխադրական շարժման ազատության յուրաքանչյուր աստիճանի համար կա մի մեծություն գազի համար, որը հավասար է գազի համընդհանուր հաստատունի կեսին:

Հետաքրքիր փաստեր
Միատոմ գազի մասնիկը ենթադրվում է, որ ունի ազատության երեք փոխակերպման աստիճան, ուստի գազի հատուկ ջերմությունն ունի ազատության երեք, երկու պտտվող և մեկ թրթռումային աստիճան: Դրանց միատեսակ բաշխման օրենքը հանգեցնում է մշտական ծավալով հատուկ ջերմության հավասարմանը R.
Փորձերի ընթացքում պարզվել է, որ երկատոմային գազի ջերմունակությունը համապատասխանում է R արժեքին։ Տեսության և պրակտիկայի միջև նման անհամապատասխանությունը բացատրվում է նրանով, որ իդեալական գազի ջերմունակությունը կապված է քվանտի հետ։ հետևաբար, հաշվարկներ կատարելիս կարևոր է օգտագործել վիճակագրություն՝ հիմնված քվանտի վրամեխանիկա.
Հիմք ընդունելով քվանտային մեխանիկայի հիմունքները, մասնիկների ցանկացած համակարգ, որը տատանվում կամ պտտվում է, ներառյալ գազի մոլեկուլները, ունի էներգիայի միայն որոշ դիսկրետ արժեքներ:
Եթե համակարգում ջերմային շարժման էներգիան բավարար չէ որոշակի հաճախականության տատանումներ գրգռելու համար, ապա այդպիսի շարժումները չեն նպաստում համակարգի ընդհանուր ջերմային հզորությանը։
Արդյունքում ազատության որոշակի աստիճանը դառնում է «սառեցված», դրա վրա անհնար է կիրառել հավասարաչափության օրենքը։
Գազերի ջերմունակությունը այն վիճակի կարևոր հատկանիշն է, որից կախված է ողջ թերմոդինամիկական համակարգի գործունեությունը:
Ջերմաստիճանը, որի դեպքում հավասարության օրենքը կարող է կիրառվել ազատության թրթռումային կամ պտտվող աստիճանի նկատմամբ, բնութագրվում է քվանտային տեսությամբ, կապում է Պլանկի հաստատունը Բոլցմանի հաստատունի հետ։

Դիատոմիական գազեր
Այդպիսի գազերի պտտման էներգիայի մակարդակների միջև բացերը փոքրաթիվ աստիճանի են: Բացառություն է կազմում ջրածինը, որի ջերմաստիճանի արժեքը որոշվում է հարյուրավոր աստիճաններով։
Այդ իսկ պատճառով մշտական ճնշման դեպքում գազի ջերմունակությունը դժվար է նկարագրել միասնական բաշխման օրենքով։ Քվանտային վիճակագրության մեջ ջերմունակությունը որոշելիս հաշվի է առնվում, որ դրա թրթռողական մասը ջերմաստիճանի նվազման դեպքում արագ նվազում է և հասնում զրոյի։
Այս երևույթը բացատրում է այն փաստը, որ սենյակային ջերմաստիճանում ջերմային հզորության գրեթե թրթռումային մաս չկա, քանի որերկատոմային գազ, այն համապատասխանում է R հաստատունին։
Գազի ջերմային հզորությունը մշտական ծավալով ցածր ջերմաստիճանի ցուցիչների դեպքում որոշվում է քվանտային վիճակագրության միջոցով։ Գոյություն ունի Ներնստի սկզբունքը, որը կոչվում է թերմոդինամիկայի երրորդ օրենք։ Ելնելով դրա ձևակերպումից՝ գազի մոլային ջերմունակությունը կնվազի ջերմաստիճանի նվազման հետ՝ ձգտելով զրոյի:

Պինդ մարմինների առանձնահատկությունները
Եթե գազերի խառնուրդի ջերմունակությունը կարելի է բացատրել քվանտային վիճակագրության միջոցով, ապա ագրեգացման պինդ վիճակի համար ջերմային շարժումը բնութագրվում է հավասարակշռության դիրքի մոտ գտնվող մասնիկների աննշան տատանումներով:
Յուրաքանչյուր ատոմ ունի ազատության երեք թրթռումային աստիճան, հետևաբար, համաձայն հավասարաչափության օրենքի, պինդ մարմնի մոլային ջերմային հզորությունը կարող է հաշվարկվել որպես 3nR, ընդ որում n-ը մոլեկուլի ատոմների թիվն է:
Գործնականում այս թիվը այն սահմանն է, որին հակված է պինդ մարմնի ջերմունակությունը բարձր ջերմաստիճաններում:
Առավելագույնը կարելի է ձեռք բերել սովորական ջերմաստիճանում որոշ տարրերի, այդ թվում՝ մետաղների համար: n=1-ի համար Դուլոնգի և Փիթի օրենքը կատարվում է, իսկ բարդ նյութերի դեպքում նման սահմանի հասնելը բավականին դժվար է։ Քանի որ իրականում սահմանը հնարավոր չէ ձեռք բերել, տեղի է ունենում պինդ նյութի քայքայումը կամ հալումը:
Քվանտային տեսության պատմություն
Քվանտային տեսության հիմնադիրներն են Էյնշտեյնը և Դեբին քսաներորդ դարի սկզբին: Այն հիմնված է ատոմների տատանողական շարժումների քվանտացման վրա որոշակիբյուրեղյա. Ցածր ջերմաստիճանի ցուցիչների դեպքում պինդ մարմնի ջերմունակությունը պարզվում է ուղիղ համեմատական է խորանարդով վերցված բացարձակ արժեքին։ Այս հարաբերությունները կոչվել են Դեբիի օրենք։ Որպես չափանիշ, որը հնարավորություն է տալիս տարբերակել ցածր և բարձր ջերմաստիճանի ցուցիչները, ընդունվում է դրանց համեմատությունը Debye ջերմաստիճանի հետ։
Այս արժեքը որոշվում է մարմնում ատոմի թրթռումների սպեկտրով, հետևաբար այն լրջորեն կախված է նրա բյուրեղային կառուցվածքի առանձնահատկություններից։
QD մի արժեք է, որն ունի մի քանի հարյուր K, բայց, օրինակ, այն շատ ավելի բարձր է ադամանդի մեջ:
Հաղորդող էլեկտրոնները զգալի ներդրում ունեն մետաղների ջերմունակության մեջ: Այն հաշվարկելու համար օգտագործվում է Ֆերմիի քվանտային վիճակագրությունը։ Մետաղների ատոմների էլեկտրոնային հաղորդունակությունը ուղիղ համեմատական է բացարձակ ջերմաստիճանին: Քանի որ դա աննշան արժեք է, այն հաշվի է առնվում միայն բացարձակ զրոյի հակված ջերմաստիճանների դեպքում։
Ջերմային հզորության որոշման մեթոդներ
Գլխավոր փորձարարական մեթոդը կալորիմետրիան է: Ջերմային հզորության տեսական հաշվարկ իրականացնելու համար օգտագործվում է վիճակագրական թերմոդինամիկա։ Այն վավեր է իդեալական գազի, ինչպես նաև բյուրեղային մարմինների համար, իրականացվում է նյութի կառուցվածքի վերաբերյալ փորձարարական տվյալների հիման վրա։
Իդեալական գազի ջերմային հզորությունը հաշվարկելու էմպիրիկ մեթոդները հիմնված են քիմիական կառուցվածքի գաղափարի վրա, ատոմների առանձին խմբերի ներդրումը Ср::
Հեղուկների համար օգտագործվում են նաև մեթոդներ, որոնք հիմնված են թերմոդինամիկայի օգտագործման վրացիկլեր, որոնք հնարավորություն են տալիս իդեալական գազի ջերմունակությունից հեղուկ անցնել գոլորշիացման գործընթացի էնթալպիայի ջերմաստիճանի ածանցյալի միջոցով:
Լուծման դեպքում ջերմային հզորության հաշվարկը որպես հավելման ֆունկցիա չի թույլատրվում, քանի որ լուծույթի ջերմունակության ավելցուկային արժեքը հիմնականում նշանակալի է։
Այն գնահատելու համար մեզ անհրաժեշտ է լուծումների մոլեկուլային-վիճակագրական տեսությունը։ Ամենադժվարը թերմոդինամիկական վերլուծության մեջ տարասեռ համակարգերի ջերմային հզորության նույնականացումն է:

Եզրակացություն
Ջերմային հզորության ուսումնասիրությունը թույլ է տալիս հաշվարկել քիմիական ռեակտորներում, ինչպես նաև քիմիական արտադրության այլ ապարատներում տեղի ունեցող գործընթացների էներգիայի հաշվեկշիռը: Բացի այդ, այս արժեքը անհրաժեշտ է հովացուցիչ նյութերի օպտիմալ տեսակների ընտրության համար:
Ներկայումս նյութերի ջերմային հզորության փորձարարական որոշումը տարբեր ջերմաստիճանային ընդմիջումներով՝ ցածր արժեքներից մինչև բարձր արժեքներ, նյութի թերմոդինամիկական բնութագրերի որոշման հիմնական տարբերակն է: Նյութի էնտրոպիան և էնթալպիան հաշվարկելիս օգտագործվում են ջերմունակության ինտեգրալներ։ Որոշակի ջերմաստիճանի միջակայքում քիմիական ռեակտիվների ջերմային հզորության մասին տեղեկատվությունը թույլ է տալիս հաշվարկել գործընթացի ջերմային ազդեցությունը: Լուծումների ջերմային հզորության մասին տեղեկատվությունը թույլ է տալիս հաշվարկել դրանց թերմոդինամիկական պարամետրերը ցանկացած ջերմաստիճանի արժեքներում վերլուծված միջակայքում:
Օրինակ՝ հեղուկը բնութագրվում է ջերմության մի մասի ծախսումով՝ պոտենցիալ էներգիայի արժեքը փոխելու համար։արձագանքող մոլեկուլներ. Այս արժեքը կոչվում է «կոնֆիգուրացիա» ջերմային հզորություն, որն օգտագործվում է լուծումները նկարագրելու համար:
Դժվար է կատարել լիարժեք մաթեմատիկական հաշվարկներ՝ հաշվի չառնելով նյութի թերմոդինամիկական բնութագրերը, նրա ագրեգացման վիճակը։ Այդ իսկ պատճառով հեղուկների, գազերի, պինդ մարմինների համար օգտագործվում է այնպիսի հատկանիշ, ինչպիսին է հատուկ ջերմային հզորությունը, ինչը հնարավորություն է տալիս բնութագրել նյութի էներգետիկ պարամետրերը։






