Առաձգականության մոդուլը ֆիզիկական մեծություն է, որը բնութագրում է նյութի առաձգական վարքը, երբ արտաքին ուժ է գործադրվում դրա վրա որոշակի ուղղությամբ: Նյութի առաձգական վարքագիծը նշանակում է դրա դեֆորմացիան առաձգական հատվածում:
Նյութերի առաձգականության ուսումնասիրության պատմություն

Առաձգական մարմինների ֆիզիկական տեսությունը և նրանց վարքագիծը արտաքին ուժերի ազդեցության տակ մանրամասն դիտարկվել և ուսումնասիրվել է 19-րդ դարի անգլիացի գիտնական Թոմաս Յանգի կողմից։ Այնուամենայնիվ, առաձգականության գաղափարը մշակվել է դեռևս 1727 թվականին շվեյցարացի մաթեմատիկոս, ֆիզիկոս և փիլիսոփա Լեոնհարդ Էյլերի կողմից, իսկ առաձգականության մոդուլի հետ կապված առաջին փորձերը կատարվել են 1782 թվականին, այսինքն՝ Թոմաս Յունգի աշխատանքից 25 տարի առաջ։ վենետիկյան մաթեմատիկոս և փիլիսոփա Յակոպո Ռիկատտիի կողմից։
Թոմաս Յանգի արժանիքը կայանում է նրանում, որ նա առաձգականության տեսությանը տվել է նուրբ ժամանակակից տեսք, որը հետագայում ձևակերպվել է պարզ, իսկ հետո ընդհանրացված Հուկի օրենքի տեսքով:
:
Առաձգականության ֆիզիկական բնույթ
Ցանկացած մարմին բաղկացած է ատոմներից, որոնց միջև գործում են ձգողական և վանող ուժերը։ Այս ուժերի հավասարակշռությունն էնյութի վիճակն ու պարամետրերը տվյալ պայմաններում։ Պինդ մարմնի ատոմները, երբ նրանց վրա կիրառվում են լարվածության կամ սեղմման աննշան արտաքին ուժեր, սկսում են տեղաշարժվել՝ առաջացնելով հակառակ ուղղությամբ և մեծությամբ հավասար ուժ, որը ձգտում է ատոմներին վերադարձնել իրենց սկզբնական վիճակին։
։
Ատոմների նման տեղաշարժման գործընթացում ամբողջ համակարգի էներգիան մեծանում է։ Փորձերը ցույց են տալիս, որ փոքր շտամների դեպքում էներգիան համաչափ է այս շտամների քառակուսու հետ: Սա նշանակում է, որ ուժը, լինելով էներգիայի նկատմամբ ածանցյալ, պարզվում է, որ համաչափ է լարման առաջին ուժին, այսինքն՝ գծայինորեն կախված է նրանից։ Պատասխանելով այն հարցին, թե որքա՞ն է առաձգականության մոդուլը, կարող ենք ասել, որ սա ատոմի վրա ազդող ուժի և այդ ուժի առաջացրած դեֆորմացիայի համաչափության գործակիցն է։ Յանգի մոդուլի չափը նույնն է, ինչ ճնշման չափը (Պասկալ):
Էլաստիկ սահման
Համաձայն սահմանման՝ առաձգականության մոդուլը ցույց է տալիս, թե որքան լարվածություն պետք է կիրառվի պինդ նյութի վրա, որպեսզի դրա դեֆորմացիան լինի 100%։ Այնուամենայնիվ, բոլոր պինդ մարմինները ունեն առաձգական սահման, որը հավասար է 1% լարման: Սա նշանակում է, որ եթե համապատասխան ուժ է կիրառվում, և մարմինը դեֆորմացվում է 1%-ից պակաս քանակով, ապա այդ ուժի ավարտից հետո մարմինը ճշգրտորեն վերականգնում է իր սկզբնական ձևն ու չափերը: Եթե կիրառվի չափազանց մեծ ուժ, որի դեպքում դեֆորմացիայի արժեքը գերազանցում է 1%-ը, արտաքին ուժի դադարեցումից հետո մարմինն այլևս չի վերականգնի իր սկզբնական չափերը: Վերջին դեպքում խոսվում է մնացորդային դեֆորմացիայի առկայության մասին, որըապացույց, որ նյութի առաձգական սահմանը գերազանցվել է։
Յանգի մոդուլը գործողության մեջ
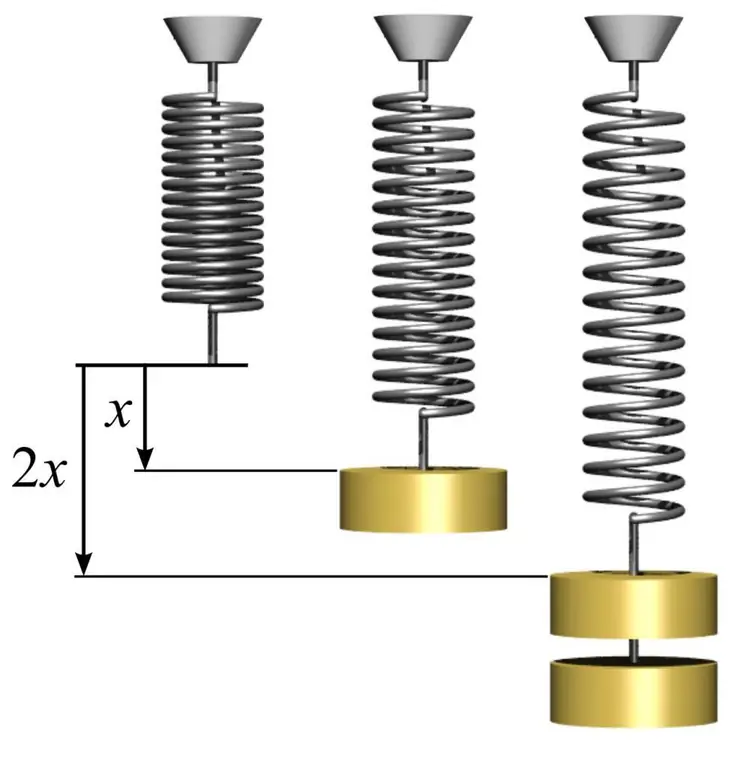
Առաձգականության մոդուլը որոշելու, ինչպես նաև այն օգտագործելու եղանակը հասկանալու համար կարող եք պարզ օրինակ բերել զսպանակով։ Դա անելու համար հարկավոր է մետաղյա զսպանակ վերցնել և չափել այն շրջանագծի տարածքը, որը կազմում է դրա պարույրները: Սա արվում է S=πr² պարզ բանաձևի միջոցով, որտեղ n-ը pi է, որը հավասար է 3,14-ի, իսկ r-ը աղբյուրի կծիկի շառավիղն է:
Հաջորդը չափեք զսպանակի երկարությունը l0 առանց բեռի: Եթե m1 զանգվածի ցանկացած բեռ կախեք զսպանակի վրա, ապա այն կավելացնի դրա երկարությունը մինչև որոշակի արժեք l1: Էլաստիկության E մոդուլը կարող է հաշվարկվել Հուկի օրենքի իմացության հիման վրա բանաձևով. E=m1gl0/(S(l 1-l0)), որտեղ g-ն ազատ անկման արագացումն է: Այս դեպքում մենք նշում ենք, որ առաձգական հատվածում աղբյուրի դեֆորմացիայի քանակը կարող է զգալիորեն գերազանցել 1%-ը։
։
Young-ի մոդուլի իմացությունը թույլ է տալիս կանխատեսել որոշակի լարվածության ազդեցության տակ դեֆորմացիայի չափը: Այս դեպքում, եթե մեկ այլ զանգված m2 կախենք զսպանակի վրա, ապա կստանանք հարաբերական դեֆորմացիայի հետևյալ արժեքը՝ d=m2g/ (SE), որտեղ d - հարաբերական դեֆորմացիա առաձգական շրջանում:
Իզոտրոպիա և անիզոտրոպիա
Առաձգականության մոդուլը նյութի բնութագիր է, որը նկարագրում է իր ատոմների և մոլեկուլների միջև կապի ուժը, սակայն որոշակի նյութը կարող է ունենալ Յանգի մի քանի տարբեր մոդուլներ։
Փաստն այն է, որ յուրաքանչյուր պինդ նյութի հատկությունները կախված են նրա ներքին կառուցվածքից:Եթե բոլոր տարածական ուղղություններով հատկությունները նույնն են, ապա խոսքը իզոտրոպ նյութի մասին է։ Նման նյութերը միատարր կառուցվածք ունեն, ուստի արտաքին ուժի ներգործությունը տարբեր ուղղություններով նրանց վրա առաջացնում է նյութի նույն ռեակցիան։ Բոլոր ամորֆ նյութերը իզոտրոպ են, ինչպիսիք են ռետինը կամ ապակին:
Անիզոտրոպիան երևույթ է, որը բնութագրվում է պինդ կամ հեղուկի ֆիզիկական հատկությունների ուղղությունից կախվածությամբ։ Դրանց վրա հիմնված բոլոր մետաղներն ու համաձուլվածքները ունեն այս կամ այն բյուրեղային ցանց, այսինքն՝ իոնային միջուկների կարգավորված, այլ ոչ թե քաոսային դասավորություն։ Նման նյութերի համար առաձգականության մոդուլը տատանվում է՝ կախված արտաքին սթրեսի գործողության առանցքից։ Օրինակ, խորանարդ սիմետրիա ունեցող մետաղները, ինչպիսիք են ալյումինը, պղինձը, արծաթը, հրակայուն մետաղները և այլն, ունեն երեք տարբեր Յանգի մոդուլներ։
Կտրման մոդուլ
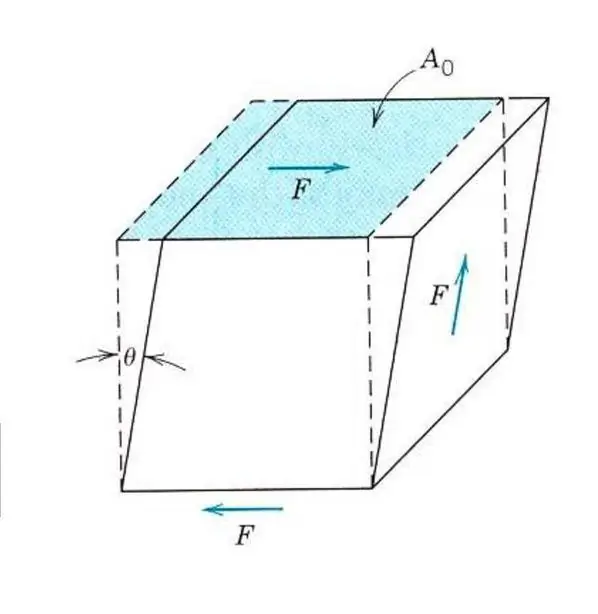
Նույնիսկ իզոտրոպ նյութի առաձգական հատկությունների նկարագրությունը չի պահանջում մեկ Յանգի մոդուլի իմացություն: Քանի որ, բացի լարումից և սեղմումից, նյութի վրա կարող են ազդել ճեղքման կամ ոլորման լարումները: Այս դեպքում արտաքին ուժին այլ կերպ կարձագանքի։ Առաձգական կտրվածքի դեֆորմացիան նկարագրելու համար ներկայացվել է Յանգի մոդուլի, ճեղման մոդուլի կամ երկրորդ տեսակի առաձգականության մոդուլի անալոգը:
Բոլոր նյութերը դիմադրում են կտրվածքային լարումներին ավելի քիչ, քան լարվածությունը կամ սեղմումը, հետևաբար նրանց կտրվածքի մոդուլի արժեքը 2-3 անգամ փոքր է Յանգի մոդուլի արժեքից: Այսպիսով, տիտանի համար, որի Յանգի մոդուլը հավասար է 107 ԳՊա, կտրվածքի մոդուլը հավասար է.ընդամենը 40 ԳՊա, պողպատի համար այս թվերը համապատասխանաբար 210 ԳՊա և 80 ԳՊա են։
Փայտի առաձգականության մոդուլ

Փայտը անիզոտրոպ նյութ է, քանի որ փայտի մանրաթելերը ուղղված են որոշակի ուղղությամբ: Հենց մանրաթելերի երկայնքով է չափվում փայտի առաձգականության մոդուլը, քանի որ այն 1-2 կարգով փոքր է մանրաթելերի միջով: Փայտի համար Յանգի մոդուլի իմացությունը կարևոր է և հաշվի է առնվում փայտե պանելային կառույցների նախագծման ժամանակ:
Փայտի առաձգականության մոդուլի արժեքները որոշ տեսակի ծառերի համար ներկայացված են ստորև բերված աղյուսակում:
| Ծառի տեսք | Յանգի մոդուլը GPa-ում |
| Դափնու ծառ | 14 |
| էվկալիպտ | 18 |
| Cedar | 8 |
| Սպռուս | 11 |
| Pine | 10 |
| Կաղնու | 12 |
Հարկ է նշել, որ տվյալ ծառի համար տրված արժեքները կարող են տարբերվել մինչև 1 ԳՊա-ով, քանի որ նրա Յանգի մոդուլը ազդում է փայտի խտությունից և աճի պայմաններից:

Կտրման մոդուլները տարբեր ծառատեսակների համար գտնվում են 1-2 ԳՊա միջակայքում, օրինակ՝ սոճու համար այն կազմում է 1,21 ԳՊա, իսկ կաղնու համար՝ 1,38 ԳՊա, այսինքն՝ փայտը գործնականում չի դիմադրում կտրվածքային լարումներին: Այս հանգամանքը պետք է հաշվի առնել փայտե կրող կառույցների արտադրության ժամանակ, որոնք նախատեսված են միայն լարվածության կամ սեղմման պայմաններում աշխատելու համար։
Մետաղների առաձգական բնութագրերը
Երբ համեմատվում է Յանգի փայտի մոդուլի հետ, մետաղների և համաձուլվածքների համար այս արժեքի միջին արժեքները մեծության կարգով ավելի մեծ են, ինչպես ցույց է տրված հետևյալ աղյուսակում:
| Մետաղ | Յանգի մոդուլը GPa-ում |
| Բրոնզ | 120 |
| պղինձ | 110 |
| Պողպատ | 210 |
| Տիտանի | 107 |
| Նիկել | 204 |
Մետաղների առաձգական հատկությունները, որոնք ունեն խորանարդ սինգոնիա, նկարագրվում են երեք առաձգական հաստատուններով: Այդպիսի մետաղներից են պղինձը, նիկելը, ալյումինը, երկաթը։ Եթե մետաղն ունի վեցանկյուն սինգոնիա, ապա դրա առաձգական բնութագրերը նկարագրելու համար արդեն վեց հաստատուն է անհրաժեշտ։
Մետաղական համակարգերի համար Յանգի մոդուլը չափվում է 0,2% լարվածության սահմաններում, քանի որ մեծ արժեքներ արդեն կարող են առաջանալ ոչ առաձգական շրջանում:






