Թերմոդինամիկայի կարևոր բաժինը նյութի տարբեր փուլերի միջև փոխակերպումների ուսումնասիրությունն է, քանի որ այդ գործընթացները տեղի են ունենում գործնականում և հիմնարար նշանակություն ունեն որոշակի պայմաններում համակարգի վարքագիծը կանխատեսելու համար: Այս փոխակերպումները կոչվում են փուլային անցումներ, որոնց նվիրված է հոդվածը։
Ֆազի և համակարգի բաղադրիչի հայեցակարգը

Ֆիզիկայի մեջ փուլային անցումների քննարկմանը անցնելուց առաջ անհրաժեշտ է սահմանել բուն փուլի հասկացությունը: Ինչպես հայտնի է ընդհանուր ֆիզիկայի դասընթացից, գոյություն ունի նյութի երեք վիճակ՝ գազային, պինդ և հեղուկ։ Գիտության հատուկ բաժնում՝ թերմոդինամիկայում, օրենքները ձևակերպված են նյութի փուլերի, այլ ոչ թե դրանց ագրեգացման վիճակների համար։ Փուլը հասկացվում է որպես նյութի որոշակի ծավալ, որն ունի միատարր կառուցվածք, բնութագրվում է հատուկ ֆիզիկական և քիմիական հատկություններով և մնացած նյութից բաժանված է սահմաններով, որոնք կոչվում են միջփուլ:
:
Այսպիսով, «փուլ» հասկացությունը կրում է շատ ավելի գործնականորեն կարևոր տեղեկություններ հատկությունների մասիննյութ, քան դրա ագրեգացման վիճակը: Օրինակ՝ երկաթի նման մետաղի պինդ վիճակը կարող է լինել հետևյալ փուլերում՝ ցածր ջերմաստիճանի մագնիսական մարմնի կենտրոնացված խորանարդ (BCC), ցածր ջերմաստիճանի ոչ մագնիսական bcc, դեմքի կենտրոնացված խորանարդ (fcc) և բարձր- ջերմաստիճանը ոչ մագնիսական BCC.
Բացի «փուլ» հասկացությունից, թերմոդինամիկայի օրենքներում օգտագործվում է նաև «բաղադրիչներ» տերմինը, որը նշանակում է որոշակի համակարգ կազմող քիմիական տարրերի քանակը։ Սա նշանակում է, որ փուլը կարող է լինել կամ միաբաղադրիչ (1 քիմիական տարր) կամ բազմաբաղադրիչ (մի քանի քիմիական տարր):
Գիբսի թեորեմ և հավասարակշռություն համակարգի փուլերի միջև

Փուլային անցումները հասկանալու համար անհրաժեշտ է իմանալ դրանց միջև եղած հավասարակշռության պայմանները: Այս պայմանները կարելի է մաթեմատիկորեն ստանալ՝ լուծելով Գիբսի հավասարումների համակարգը դրանցից յուրաքանչյուրի համար՝ ենթադրելով, որ հավասարակշռության վիճակը հասնում է, երբ արտաքին ազդեցությունից մեկուսացված համակարգի ընդհանուր Գիբսի էներգիան դադարում է փոխվել։
Հավասարումների նշված համակարգի լուծման արդյունքում պայմաններ են ձեռք բերվում մի քանի փուլերի միջև հավասարակշռության գոյության համար. մեկուսացված համակարգը կդադարի զարգանալ միայն այն դեպքում, երբ յուրաքանչյուր բաղադրիչի ճնշումները, քիմիական պոտենցիալները և ջերմաստիճանները բոլոր փուլերում։ հավասար են միմյանց։
Գիբսի փուլային կանոն հավասարակշռության համար

Մի քանի փուլերից և բաղադրիչներից բաղկացած համակարգը կարող է հավասարակշռության մեջ լինել ոչ միայնորոշակի պայմաններում, օրինակ, որոշակի ջերմաստիճանի և ճնշման դեպքում: Հավասարակշռության համար Գիբսի թեորեմի որոշ փոփոխականներ կարող են փոփոխվել՝ պահպանելով և՛ փուլերի, և՛ բաղադրիչների քանակը, որոնք գտնվում են այս հավասարակշռության մեջ: Փոփոխականների թիվը, որոնք կարող են փոփոխվել առանց համակարգում հավասարակշռությունը խախտելու, կոչվում է այս համակարգի ազատությունների թիվ։
F փուլերից և k բաղադրիչներից բաղկացած համակարգի l ազատությունների թիվը եզակիորեն որոշվում է Գիբսի փուլային կանոնից: Այս կանոնը մաթեմատիկորեն գրված է հետևյալ կերպ. l + f=k + 2. Ինչպե՞ս աշխատել այս կանոնի հետ: Շատ պարզ. Օրինակ, հայտնի է, որ համակարգը բաղկացած է f=3 հավասարակշռության փուլերից։ Ո՞րն է բաղադրիչների նվազագույն քանակը, որը կարող է պարունակել նման համակարգը: Հարցին կարող եք պատասխանել հետևյալ պատճառաբանությամբ՝ հավասարակշռության դեպքում ամենախիստ պայմանները գոյություն ունեն, երբ այն իրականացվում է միայն որոշակի ցուցանիշներով, այսինքն՝ ցանկացած թերմոդինամիկական պարամետրի փոփոխությունը կհանգեցնի անհավասարակշռության։ Սա նշանակում է, որ ազատությունների թիվը l=0։ Փոխարինելով l-ի և f-ի հայտնի արժեքները՝ մենք ստանում ենք k=1, այսինքն՝ համակարգ, որտեղ երեք փուլերը գտնվում են հավասարակշռության մեջ, կարող է բաղկացած լինել մեկ բաղադրիչից։ Հիմնական օրինակը ջրի եռակի կետն է, որտեղ սառույցը, հեղուկ ջուրը և գոլորշին հավասարակշռված են որոշակի ջերմաստիճաններում և ճնշումներում:
Ֆազային փոխակերպումների դասակարգում
Եթե դուք սկսեք փոխել որոշ թերմոդինամիկական պարամետրեր հավասարակշռության մեջ գտնվող համակարգում, կարող եք դիտել, թե ինչպես մի փուլ կվերանա, իսկ մյուսը կհայտնվի: Այս գործընթացի պարզ օրինակը սառույցի հալումն է, երբ այն տաքացվում է:
Հաշվի առնելով, որ Գիբսի հավասարումը կախված է միայն երկու փոփոխականներից (ճնշում և ջերմաստիճան), և փուլային անցումը ներառում է այս փոփոխականների փոփոխությունը, ապա մաթեմատիկորեն փուլերի միջև անցումը կարելի է նկարագրել Գիբսի էներգիան դրա նկատմամբ տարբերելով։ փոփոխականներ. Հենց այս մոտեցումն է կիրառվել ավստրիացի ֆիզիկոս Փոլ Էրենֆեստի կողմից 1933 թվականին, երբ նա կազմել է բոլոր հայտնի թերմոդինամիկական գործընթացների դասակարգումը, որոնք տեղի են ունենում փուլային հավասարակշռության փոփոխությամբ:
Թերմոդինամիկայի հիմունքներից հետևում է, որ Գիբսի էներգիայի առաջին ածանցյալը ջերմաստիճանի նկատմամբ հավասար է համակարգի էնտրոպիայի փոփոխությանը։ Գիբսի էներգիայի ածանցյալը ճնշման նկատմամբ հավասար է ծավալի փոփոխությանը։ Եթե, երբ համակարգի փուլերը փոխվում են, էնտրոպիան կամ ծավալը ընդմիջվում են, այսինքն՝ կտրուկ փոխվում են, ապա խոսում են առաջին կարգի փուլային անցման մասին։
Այնուհետև, Գիբսի էներգիայի երկրորդ ածանցյալները ջերմաստիճանի և ճնշման նկատմամբ համապատասխանաբար ջերմային հզորությունն են և ծավալային ընդարձակման գործակիցը: Եթե փուլերի միջև փոխակերպումն ուղեկցվում է նշված ֆիզիկական մեծությունների արժեքների ընդհատումով, ապա խոսվում է երկրորդ կարգի փուլային անցման մասին։
Փուլերի միջև փոխակերպումների օրինակներ

Բնության մեջ կան հսկայական թվով տարբեր անցումներ: Այս դասակարգման շրջանակներում առաջին տեսակի անցումների վառ օրինակներ են մետաղների հալման կամ օդից ջրային գոլորշիների խտացման գործընթացները, երբ համակարգում առկա է ծավալային թռիչք։
։
Եթե խոսենք երկրորդ կարգի անցումների մասին, ապա վառ օրինակներ են երկաթի փոխակերպումը մագնիսականից պարամագնիսական վիճակի ջերմաստիճանում։768 ºC կամ մետաղական հաղորդիչի փոխակերպումը գերհաղորդիչ վիճակի բացարձակ զրոյին մոտ ջերմաստիճանում:
Հավասարումներ, որոնք նկարագրում են առաջին տեսակի անցումները
Գործնականում հաճախ անհրաժեշտ է իմանալ, թե ինչպես են ջերմաստիճանը, ճնշումը և կլանված (ազատված) էներգիան փոխվում համակարգում, երբ դրանում տեղի են ունենում ֆազային փոխակերպումներ: Այս նպատակով օգտագործվում են երկու կարևոր հավասարումներ. Դրանք ստացվում են թերմոդինամիկայի հիմունքների իմացության հիման վրա՝
- Կլապեյրոնի բանաձևը, որը հաստատում է ճնշման և ջերմաստիճանի միջև կապը տարբեր փուլերի միջև փոխակերպումների ժամանակ:
- Clausius բանաձևը, որը կապում է կլանված (ազատված) էներգիան և համակարգի ջերմաստիճանը փոխակերպման ընթացքում:
Երկու հավասարումների օգտագործումը ոչ միայն ֆիզիկական մեծությունների քանակական կախվածություններ ստանալու համար է, այլ նաև ֆազային դիագրամների վրա հավասարակշռության կորերի թեքության նշանը որոշելու համար:
Հավասարում երկրորդ տեսակի անցումները նկարագրելու համար

1-ին և 2-րդ տեսակի փուլային անցումները նկարագրվում են տարբեր հավասարումներով, քանի որ Կլաուզիուսի և Կլաուզիուսի հավասարումների կիրառումը երկրորդ կարգի անցումների համար հանգեցնում է մաթեմատիկական անորոշության:
Վերջինս նկարագրելու համար օգտագործվում են Էրենֆեստի հավասարումները, որոնք կապ են հաստատում ճնշման և ջերմաստիճանի փոփոխությունների միջև փոխակերպման գործընթացում ջերմային հզորության և ծավալային ընդլայնման գործակցի փոփոխությունների իմացության միջոցով: Էրենֆեստի հավասարումները օգտագործվում են հաղորդիչ-գերհաղորդիչ անցումները նկարագրելու համար մագնիսական դաշտի բացակայության դեպքում:
Կարևորությունփուլային դիագրամներ
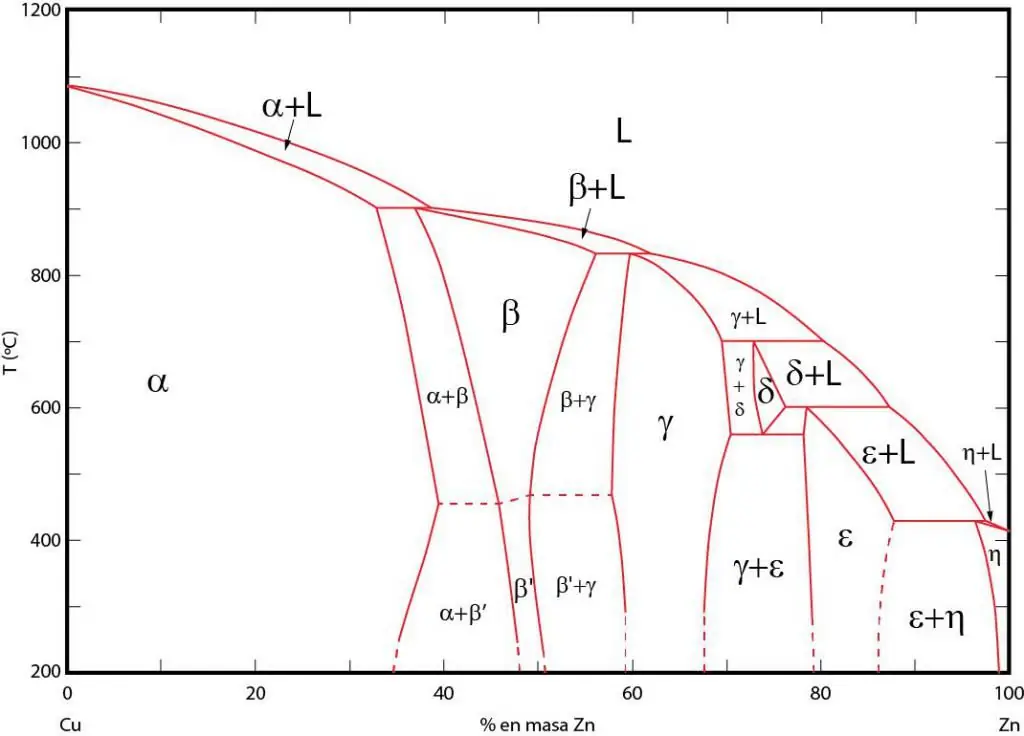
Փուլային դիագրամները այն տարածքների գրաֆիկական ներկայացումն են, որոնցում համապատասխան փուլերը գոյություն ունեն հավասարակշռության մեջ: Այս տարածքները բաժանված են փուլերի միջև հավասարակշռության գծերով: Հաճախ օգտագործվում են P-T (ճնշում-ջերմաստիճան), T-V (ջերմաստիճան-ծավալ) և P-V (ճնշում-ծավալ) փուլային դիագրամներ:
Ֆազային դիագրամների կարևորությունը կայանում է նրանում, որ դրանք թույլ են տալիս կանխատեսել, թե որ փուլում կլինի համակարգը, երբ արտաքին պայմանները համապատասխանաբար փոխվեն: Այս տեղեկատվությունը օգտագործվում է տարբեր նյութերի ջերմային մշակման ժամանակ՝ ցանկալի հատկություններով կառուցվածք ստանալու համար:






